NAND-Schaltung aus Wahrheitstabelle
Wir haben im Praktikum Alles NAND, ODER? das logische OR und XOR kennengelernt. Das OR haben wir mit NAND-Gattern realisiert. Die Umwandlung von OR in eine NAND-Schaltung ist uns nur mit Tricks gelungen.
Hier werden wir ein Verfahren anwenden, mit dem wir aus einer Wahrheitstabelle die zugehörige NAND-Schaltung entwickelt können. Dazu verwenden wir das Programm LogicBuddy.
XOR als NAND-Schaltung
Als Beispiel werden wir XOR als NAND-Schaltung realisieren.
Zuerst stellen wir die Wahrheitstabelle für XOR auf:
| A | B | E |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Tabelle 1: XOR
Wir bezeichnen die Eingänge A und B als Variablen und den Ausgang E als Ergebnis oder Funktion. Die Variablen werden mit den Eingängen unserer Schaltung verbunden. Das Ergebnis soll der Ausgang unserer Schaltung liefern. Deshalb sprechen wir oft von den Eingangsvariablen A und B und der Ausgangsvariablen E.
Berechnung mit LogicBuddy
Diese Wahrheitstabelle wird durch das Programm LogicBuddy in eine Formel umgewandelt. Diese Formel heißt minimierte logische Funktion. Mache sagen auch minimierter boolescher Ausdruck.
Als erstes müssen wir LogicBuddy mitteilen, wie groß unsere Wahrheitstabelle ist. Mit 
wird ein Dialog geöffnet, in dem wir die Zahl der Eingangsvariablen auf 2 und die der Funktionen (Ausgangsvariablen) auf 1 setzen.
Wir müssen noch die Namen unserer Logik eintragen:
Ein Klick auf das a in der Kopfzeile der Tabelle öffnet sich ein Dialog, in dem wir A als Namen eingeben. Ebenso tragen wir B und E ein.
Die Werte der Wahrheitstabelle können einfach geändert werden, indem wir unter E auf die entsprechenden Felder der Tabelle klicken.
Durch mehrmaliges Klicken erscheint auch der Wert d auf. Wir ignorieren ihn zunächst und geben nur 0 und 1 ein.
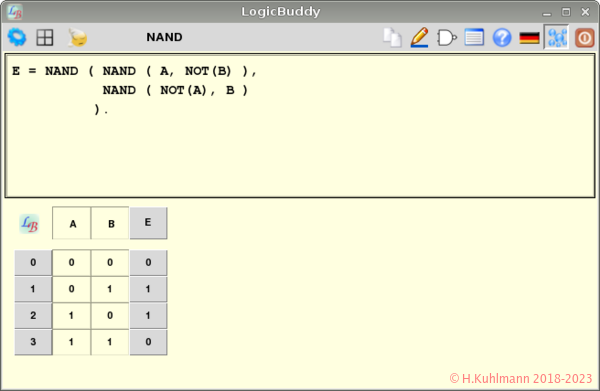
Das Ergebnis wird im oberen Fenster von LogicBuddy angezeigt:
E = NAND ( NAND ( A, NOT(B) ),
NAND ( NOT(A), B )
).
Wir sehen, dass wir drei NAND-Gatter und zwei NOT-Gatter benötigen.
Für die Realisierung beginnen wir mit der äußeren Klammer: ein NAND mit zwei Einträgen. Also ein NAND-Gatter mit zwei Eingängen (74HC00).
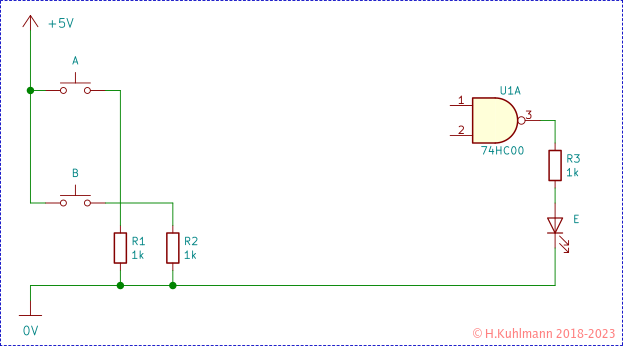
Wir gehen in die äußere Klammer hinein. Zerst finden wir oben NAND ( A, NOT(B) ), ein NAND-Gatter mit zwei Eingängen: U1B. Das Ergebnis wird mit dem Eingang (Pin 1) von U1A verbunden. Die Eingänge von U1B sind mit A und NOT B verbunden (also B über einen Inverter 4049).
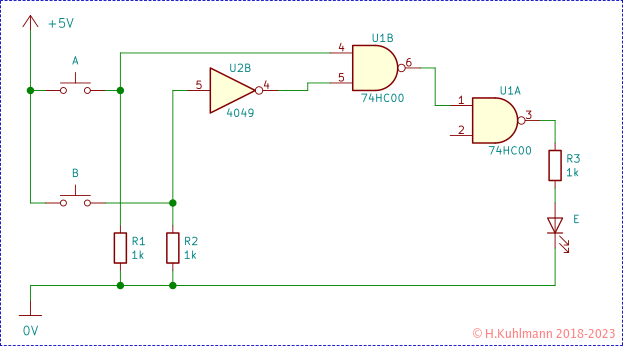
In der Klammer der logischen Formel folgt ein weiteres NAND, mit NAND ( NOT(A), B ).
Damit ist die logische Formel vollständig implementiert. Die Eingänge von U1C sind mit NOT A und B verbunden (also A über einen Inverter 4049).
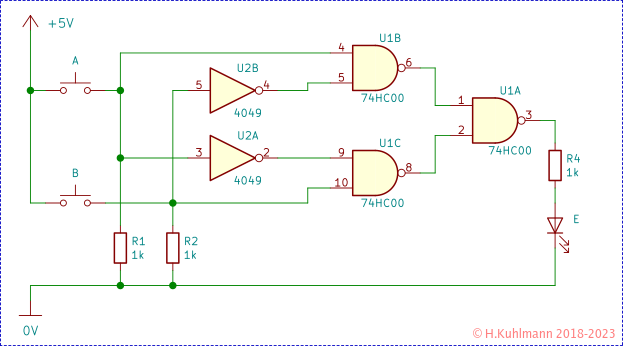
Die Schaltung ist fertiggestellt.
Im Schaltbild werden oft die Versorgungsanschlüsse und die Belegung der offenen Eingänge nicht dargestellt. Diese müssen wir vor dem Aufbau der Schaltung ergänzen.
In Bild 4 sind der Vollständigkeit halber alle übrigen Anschlüsse der ICs dargestellt. Die Stromversorgung ist angeschlossen. Alle Eingänge sind mit +5V verbunden. Es kann auch 0V sein. Die Ausgänge bleiben offen.
Zusammenfassung
Was haben wir gemacht?
Zuerst haben wir eine Wahrheitstabelle erstellt.
Dann haben wir mit LogicBuddy die minimierte logische Funktion der Wahrheitstabelle berechnet.
Für jedes NAND in der logischen Funktion haben wir ein NAND-Gatter verwendet und die Eingänge gegebenenfalls über NOT-Gatter damit verbunden. Alle Ausgänge dieser NAND-Gatter haben wir mit dem NAND-Gatter für den Ausgang angeschlossen.
Ergebnisse von LogicBuddy
Die Ergebnisse von LogicBuddy sehen für jede Ausgangsvariable so aus wie
E = NAND ( NAND ( A, NOT(B) ),
NAND ( NOT(A), B )
).
Für die Ausgangsvariable gibt es nur ein einziges NAND-Gatter. Dieses Ergebnis-NAND kann mehrere Eingänge haben.
In der Klammer hinter dem Ergebnis-NAND stehen NAND-Gatter, deren Eingänge eine oder mehrere Eingangsvariablen der Wahrheitstabelle sind. Die Eingangsvariablen sind manchmal negiert (NOT).
Dies ist die minimierte logische Funktion:
- Für jeden Ausgang liegen zwei NAND-Gatter hintereinander.
- Eingänge können negiert sein.
Software