Alles NAND, ODER?
Bisher haben wir uns nur mit NAND-Gattern beschäftigt. Sie sind eine technische Realisierung der logischen Funktion Und. Nicht ganz, sonst hieße es ja AND und nicht NAND ( NOT AND ).
Wir rekapitulieren die Wahrheitstabelle eines NAND-Gatters mit zwei Eingängen E1 und E2 und dem Ausgang A.
| E1 | E2 | A |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Tabelle 1: NAND
Alltägliche Logik
Wir alle können mit Logik umgehen. Wir benutzen sie täglich, ohne viel darüber nachzudenken. Natürlich beherrschen wir sie auch. In den folgenden Abschnitten machen wir uns unser Wissen bewusst und wenden es an. Wir werden es auch technisch umsetzen. In einem weiteren Praktikum werden wir lernen, komplizierte logische Zusammenhänge zu beschreiben und technisch umzusetzen. Eines können wir jetzt schon vorwegnehmen:
- Wir brauchen nur NAND-Gatter!
Logik in der Sprache
Wenn wir etwas mitteilen wollen, ist eines der am häufigsten verwendeten Wörter das und.
Wenn wir sagen:
Kurt und Liesel stehen auf der Brücke.
Dann wissen wir, was damit gemeint ist. Wenn das nicht der Fall ist, sagen wir:
Du irrst dich. Das ist falsch. Das ist nicht wahr.
Das kennen wir schon: wahr, falsch, nicht wahr:
wahr = 1 falsch = 0
Als Techniker wenden wir unser Wissen an und schreiben eine Wahrheitstabelle:
| Kurt | Liesel | Kurt UND Liesel stehen auf der Brücke |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Tabelle 2: UND
Das ist natürlich kein NAND. Es ist NICHT NAND. Es ist NOT NAND, genauer gesagt NAND NOT. Diese logische Funktion nennen wir AND.
Wir erinnern uns: NOT erhalten wir, wenn wir alle Eingänge eines NAND-Gatters miteinander verbinden. Unsere Schaltung ist also:
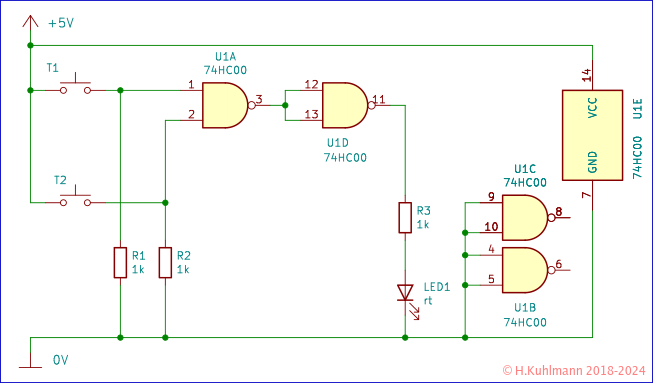
Wenn Kurt auf der Brücke ist, betätigen wir den Taster T1, für Liesel T2. Das Ergebnis wird mit LED2 angezeigt.
Wir haben ein AND mit NAND-Gattern gebaut.
Oder in der Sprache
Eine weitere einfache Aussage lautet
Kurt oder Liesel sind auf der Brücke.
Eine gute Übung: Jeder erstellt die Wahrheitstabelle für ODER
| Kurt | Liesel | Kurt ODER Liesel stehen auf der Brücke |
| 0 | 0 | ? |
| 0 | 1 | ? |
| 1 | 0 | ? |
| 1 | 1 | ? |
Tabelle 3: ODER?
Ist doch klar:
- Wenn beide nicht auf der Brücke sind, ist die Aussage falsch.
- Wenn Kurt allein auf der Brücke ist, ist die Aussage wahr.
- Wenn Liesel allein auf der Brücke ist, ist die Aussage wahr.
-
Wenn Kurt und Liesel beide auf der Brücke sind, ist die Aussage falsch.
Ist die Aussage wahr? Einige denken, dass die Aussage wahr ist.
Wir sind uns nicht ganz sicher, ob die Aussage 4 wahr oder falsch ist. Die meisten von uns haben noch nie darüber nachgedacht. Wir müssen hier eine Lösung finden. Sie ist einfach. Es gibt zwei Arten von ODER:
-
Beim inklusiven ODER ist das Ergebnis auch wahr, wenn beide auf der Brücke sind.
Beim inklusiven ODER schreiben wir OR.
-
Beim exklusiven ODER ist das Ergebnis falsch, wenn beide auf der Brücke sind.
Beim exklusiven ODER schreiben wir EXOR. Damit meinen wir: entweder - oder.
Nun zu den Wahrheitstabellen:
| K | L | OR |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Tabelle 4: OR
| K | L | EXOR |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Tabelle 5: EXOR
Oder Logik
Wir stellen uns die Frage: Wie bauen wir eine Schaltung für OR?
Überspringen
- Die folgende Bestimmung der Schaltung für OR ist nichts für Einsteiger. Sie wird viele eher abschrecken.
- Am besten überspringt man diesen Abschnitt zunächst und schaut sich einfach das Ergebnis für bei OR aus NAND an.
Danach sind die Überlegungen etwas leichter nachvollziehbar.
- Die gute Nachricht ist, dass wir später ein Programm benutzen werden, um eine logische Schaltung zu bestimmen.
Stellen wir OR und NAND in einer gemeinsamen Tabelle dar.
| K | L | NAND | OR |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
Tabelle 6: NAND und OR
Stellen wir zunächst einige Überlegungen an.
- Betrachten wir die Ausgänge, so sind die erste und die vierte Zeile vertauscht.
- Betrachten wir die Eingänge, so sind die Werte der ersten und der vierten Zeile negiert.
Eigentlich sind sie keine Lösung für unser Problem, aber sie bringen uns auf die Idee, es mit der Negation zu versuchen. Den Ausgangs zu negieren bringt offensichtlich nichts.
Versuchen wir, die Eingänge zu negieren.
Das bedeutet, vor jeden Eingang ein NOT zu setzen.
Logiker sind schreibfaul und setzen statt NOT ein Dach ^ vor den Namen des logischen Zustands, also statt NOT K, schreiben wir ^K.
Wir kennen noch eine andere Darstellung für einen negierten Wert: NOT W = W
Entsprechend den obigen Überlegungen werden in Tabelle 6 zwei neue Spalten für K und L eingefügt.
Außerdem ersetzen wir K NAND L durch K NAND L. Um ^K AND ^L zu berechnen, nehmen wir die Werte aus den Spalten K und L und tragen die Werte aus der NAND-Tabelle (1) ein.
| K | L | K | L | K NAND L | K OR L |
| 0 | 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 1 | 1 |
Tabelle 7: OR aus NAND und NOT
Und das Ergebnis ist, dass K NAND L mit K OR L übereinstimmt.
Es gilt also
K OR L = (NOT K) NAND (NOT L) K OR L = NOT ( (NOT K) AND (NOT L) ) K OR L = K NAND L K OR L = K AND L
Verwirrend und unübersichtlich?
Das finden auch manche Logiker. Deshalb schreiben sie:
K + L = ^( ^K * ^L )
Sieht aus wie eine Formel mit Addition und Multiplikation.
Oft wird eine Schreibweise verwendet, die noch übersichtlicher ist
K + L = K * L
Die folgende Tabelle fasst einige Schreibweisen zusammen.
| Bezeichnung | Symbol | Beispiel | Alternative |
| NOT | ^ | ^A | A |
| AND | * | A * B | |
| OR | + | A + B | |
| NAND | ^( A * B ) | A * B | |
| NOR | ^( A + B ) | A + B |
Tabelle 8: Logische Symbole
Die obigen Überlegungen sind zwar nicht einfach, aber mit Wahrheitstabellen war es zu bewältigen.
Keine Angst, wir müssen nicht immer solche Klimmzüge machen.
Im nächsten Praktikum werden wir lernen, wie wir mithilfe eines Programms beliebige logische Funktionen in NAND-Logiken umwandeln können.
Unsere Erkenntnis
K OR L = NOT ( (NOT K) AND (NOT L) )
oder
K + L = ^( ^K * ^L )
oder
K + L = K * L
ist sehr wichtig.
Wir können ein OR-Gatter erzeugen, indem wir
- vor jeden Eingang eines NAND-Gatters ein NOT
setzen.
- Dadurch ist es möglich, jede logische Schaltung ausschließlich mit NAND- und NOT-Gattern aufzubauen.
Überstrich für NOT
Die Schreibweise mit dem Überstrich für die Invertierung (NOT) eines Ausdrucks
NOT A = A
oder
K + L = K * L
wird oft für logische Ausdrücke verwendet. Klammern sind nicht notwendig.
Allerdings kann diese Darstellung in Standard-Textsystemen nicht ohne weiteres erzeugt werden.
Ein einfacher Überstrich ist möglich, für mehrere Überstriche oft einige Klimmzüge nötig.
OR aus NAND
Wir wollen Elektronik bauen. Also bauen wir ein OR aus NAND-Gattern auf.
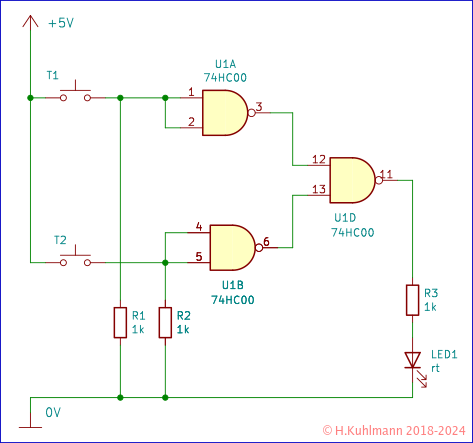
Wir brauchen drei NAND-Gatter des 74HC00, um ein OR zu bilden.
Wir sollten die Schaltung auf dem Steckboard aufbauen und überprüfen, ob das Ergebnis mit der Wahrheitstabelle für OR übereinstimmt. Wer möchte, kann noch LEDs an die Ausgänge der Zwischenergebnisse ( 3, 6 ) anschließen und mithilfe der Tabelle 7 überprüfen.
In Bild 2 sind die Stromversorgungen der Chips sowie die nicht benutzten Eingänge von U1C nicht eingezeichnet.
- Konvention:
- Die Stromversorgungen der Bauteile müssen nicht dargestellt werden.
- Alle nicht benutzten Anschlüsse werden mit 0V oder 5V verbunden.
NOR
Wenn es NAND gibt, muss es auch NOR geben. Ein NAND ist ein AND mit einem NOT dahinter. Ein NOR ist dann ein OR mit einem NOT dahinter.
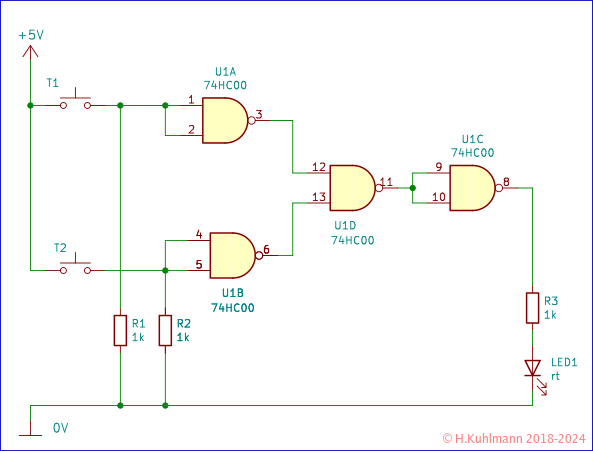
Für die bisher behandelten logischen Funktionen gibt es IC's mit diesen Funktionen. Natürlich gibt es auch die entsprechenden Symbole.
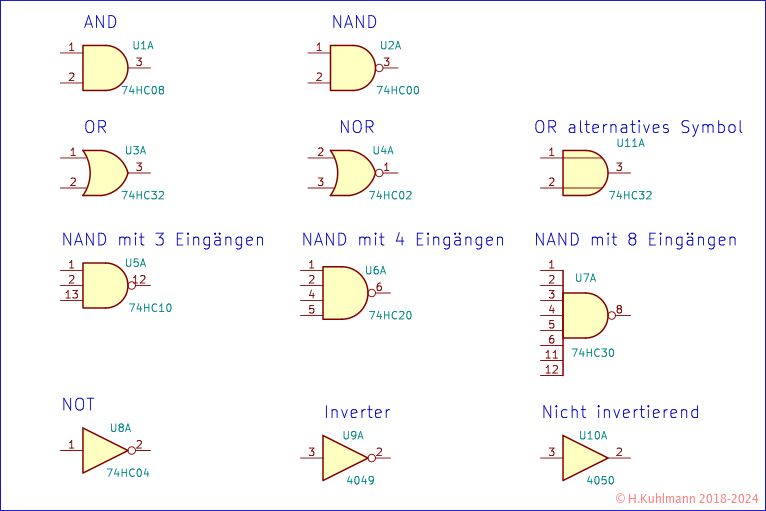
In Bild 5 zeigt die wichtigsten logischen Symbole. Außerdem sind die Bezeichnungen der verwendeten ICs angegeben
Da NAND-Gatter wichtig sind, sind auch die verfügbaren Versionen mit drei, vier und acht Eingängen aufgeführt.
Für OR und NOR-Gatter gibt es zwei Symbole mit der gleicher Bedeutung.
Es gibt auch noch NOT. Hier sind die beiden interessanten CMOS-Bausteine 74HC04 und 4049 dargestellt. Wir werden wahrscheinlich meistens den 4049 verwenden, weil er robuster und universeller ist. Die logische Funktion ist NOT. Der Begriff Inverter bedeutet dasselbe.
Der 4050 klingt wie ein Witz. Logisch ist er das auch: Er hat keine Wirkung. Elektrisch ist das anders. Wir können ihn z.B. verwenden, wenn wir einen Logikausgang für höhere Lasten brauchen. Ein 74HC00 geht schon lange in die Knie, während der 4050 noch gut funktioniert.
Der 4049 hat übrigens ähnliche elektrische Eigenschaften.
Interessant ist der Unterschied zwischen den Symbolen von AND und NAND sowie OR und NOR. Das NOT wird durch einen kleinen Kreis am Ausgang beschrieben.
Regeln
- Logische Funktionen werden durch Wahrheitstabellen beschrieben.
- Es gibt ein inklusives oder OR und ein exklusives EXOR.
- In der Logik wird meistens das inklusive OR verwendet.
- Für ein NOT werden alle Anschlüsse eines NAND-Gatters zusammengeschlossen und als Eingang verwendet.
- NOT hinter NOT ergibt die Identität. NOT hinter NOT kann entfallen.
- Ein AND ist ein NAND-Gatter, hinter dem ein NOT liegt.
- Ein OR wird aus NAND-Gattern gebildet, indem vor jeden Eingang des NAND ein NOT geschaltet wird.
- Ein NOR, also NOT OR kann wie ein OR aus NAND-Gattern aufgebaut werden.
Dabei wird vor jeden jeden Eingang des NAND ein NOT und hinter den Ausgang ein weiteres NOT geschaltet.
- Für AND, OR und NOT gibt es Symbole.
-
NOT wird durch einen kleinen Kreis dargestellt.
Dadurch wird AND zu NAND und OR zu NOR.
- Leider gibt es keine einheitliche Schreibweise für Logik: Logisches Babylon
- Wir verwenden hier die Schreibweise
- A OR B = NOT ( (NOT A) AND (NOT B) ) = (NOT A) NAND (NOT B)
- Konvention:
- Die Stromversorgung von Bauelementen muss nicht dargestellt werden.
- Alle nicht benutzten Anschlüsse werden entweder mit 0V oder mit 5V verbunden.
Fazit
Bisher konnten wir alle Logiken mit NAND-Gattern aufbauen.
Wirklich? Und was ist mit EXOR? Das sehen wir uns im nächsten Praktikum an.