Binärzähler

Die folgenden Schaltungen haben einen Takt-Eingang, der an einen entprellten Taster angeschlossen werden muss. Dazu wird besten das Takt-Modul verwendet.

Mit dem Reset-Taster wird die Schaltung in einen definierten Zustand gebracht: Er setzt alle Ausgänge auf 0.

Im Praktikum Johnson-Zähler haben wir einen einfachen Zähler untersucht. An dieser Stelle wollen wir uns mit einem anderen Zählertyp beschäftigen, der ebenso einfach aufgebaut ist, dem Binärzähler.

Im Prinzip haben wir bereits im Praktikum Johnson-Zähler einen Binärzähler betrachtet, nämlich den einstufigen Zähler. Er ändert seinen Zustand mit jedem Takt: 0-1-0-1-. Wir wissen auch, dass die Frequenz am Ausgang des einstufigen Zählers die Hälfte der Taktfrequenz beträgt.

Wenn wir solche Zählstufen hintereinander schalten, und zwar den Takt des nächsten Zählers auf den Ausgang des vorhergehenden, dann halbiert sich die Frequenz hinter jeder Zählstufe. Wir haben einen Frequenzteiler.

Ein solcher Zähler wird Binärzähler genannt.

Betrachten wir die Anzahl der D-Flip-Flops von Zählern, um einen Frequenzteiler zu erzeugen, und vergleichen wir Binärzähler, Johnson-Zähler und Ringzähler.

Die folgende Tabelle vergleicht die Teiler von Binärzählern und Johnson-Zählern.

D-Flip-Flops	Binär	Johnson	Ring
1	2	2
2	4	4	2
3	8	6	3
4	16	8	4
5	32	10	5
6	64	12	6

Tabelle 1 Teiler für Binär-, Johnson- und Ring-Zähler

Für hohe Werte der Frequenzteilung ist ein Binärzähler effizienter, da er weniger D-Flip-Flops benötigt.

Johnson- / Binärzähler

• Beim Johnson-Zähler haben alle D-Flip-Flops einen gemeinsamen Takt.

• Beim Binärzähler erhält jedes D-Flip-Flop den Takt von seinem Vorgänger.

• Der Eingangstakt liegt am ersten D-Flip-Flop.

Einfacher Binärzähler

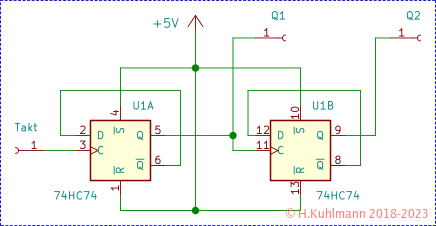
Bild 1 zeigt einen zweistufigen Binärzähler. Er besteht aus zwei D-Flip-Flops, deren invertierter Ausgang jeweils auf den Eingang zurückgekoppelt ist. Solche Schaltungen mit einzelnen D-Flip-Flops werden nur selten gebaut. Vielmehr gibt es Chips, die eine ganze Reihe solcher Zählstufen enthalten.

Mehrstufiger Binärzähler

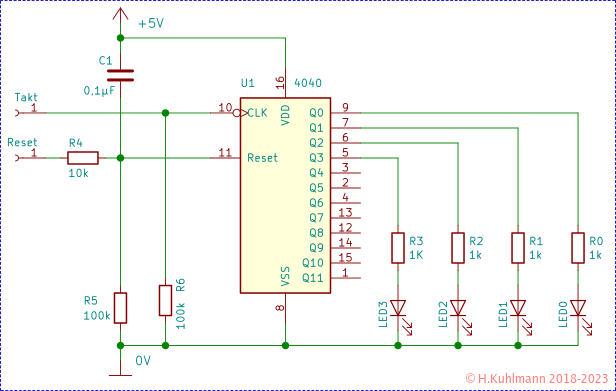
In Bild 2 zeigt der CD4040 mit 12 Binärstufen. Er besitzt nur noch einen Takteingang CLK und einen Reseteingang Reset. Der Takteingang ist invertiert, d.h. der CD4040 zählt mit der ↓ Flanke des Takts. Der Reseteingang ist nicht invertiert. Deshalb liegt der Kondensator für den automatischen Reset auf +5V.

Die ersten vier Ausgänge sind mit LEDs verbunden. Es ist sinnvoll, weitere LEDs an die Ausgänge anzuschließen. Beim Aufbau sollte die LED0 für den Ausgang Q0 ganz rechts angeordnet werden und dann weiter nach links mit den steigenden Qs. Diese Reihenfolge hilft uns später, die Schaltung zu verstehen.

Wie werden die Ausgänge bezeichnet?

Wir würden sagen, in der Reihenfolge ihres Auftretens, also gezählt.

In der Digitaltechnik gibt es immer wieder Verwirrung, weil man sich nicht einigen kann, wo man mit dem Zählen anfängt:

• beginnt man mit 1 oder

• beginnt man mit 0.

In unserem Symbol des 4040 werden die Qs ab Q0 gezählt.

Andere Symbole beginnen mit Q1

Zählerstände

Nach einem Reset durchlaufen die Ausgänge des 4040 eine bestimmte Folge.

Takt	Q3	Q2	Q1	Q0
0	0	0	0	0
1	0	0	0	1
2	0	0	1	0
3	0	0	1	1
4	0	1	0	0
5	0	1	0	1
6	0	1	1	0
7	0	1	1	1
8	1	0	0	0
9	1	0	0	1
10	1	0	1	0
11	1	0	1	1
12	1	1	0	0
13	1	1	0	1
14	1	1	1	0
15	1	1	1	1
16	0	0	0	0
17	0	0	0	1
18	0	0	1	0

Tabelle 2: Zustandsfolge der ersten vier Ausgänge

Die Folge der Zustände der ersten vier Ausgänge hat eine gewisse Systematik.

• Q0 wechselt in jedem Takt seinen Zustand 0-1-0...

• Q1 wechselt seinen Zustand mit jedem zweiten Takt.

• Q2 wechselt seinen Zustand mit jedem vierten Takt.

• Q3 wechselt seinen Zustand alle acht Takte.

• Nach sechzehn Takten wiederholt sich die Folge.

Die Systematik des Codes wird im Praktikum Binär zählen behandelt.

Dieser Zähler zeigt gut die Wirkung eines nicht entprellten Tasters.

Wenn ein Taster einfach zwischen TAKT und +5V gelegt wird, wird der Zähler beim Betätigen des Tasters meistens mehrere Schritte durchlaufen. Dies ist die Wirkung des Prellens.

Frequenzteiler

Betrachten wir die Ausgänge unter dem Gesichtspunkt der Frequenz, d.h. wie oft pro Sekunde sie ihren Zustand ändern.

Der Ausgang Q0 durchläuft die Sequenz 0-1-0 in zwei Takten. Seine Frequenz ist also halb so groß ist wie die Taktfrequenz.

Das gilt im Prinzip für jede Stufe.

Wenn f die Taktfrequenz ist, ist die Frequenz für die Ausgänge

Q0 : f1 = f / 2
Q1 : f2 = f / 4
Q2 : f3 = f / 8
Q3 : f4 = f /16

Jede Stufe des Binärzählers halbiert die Frequenz der vorhergehenden. Drei Stufen teilen die Taktfrequenz durch 2*2*2=8, vier also durch 16. Und fünf durch 32 ... zehn durch 1024.

Der 4040 ist ein Frequenzteiler der durch 2, 4, 8, 16 usw. teilt.

Solche Frequenzteiler sind sehr nützlich, wenn wir zu hohe Frequenzen haben.

Synchron - Asynchron

Bei asynchronen Zählern:

• haben alle Register (Stufen) einen anderen Takt

• den der vorhergehenden Stufe

• der CMOS 4040 ist ein asynchroner Binärzähler.

Bei synchronen Zählern

• haben alle Register (Stufen) den gleichen Takt

• ein Johnson-Zähler ist ein synchroner Zähler

• ein Johnson-Zähler zählt nicht im Binärcode

• der 74HC161 ist ein 4-Bit-Binärzähler

• der 74HC161 zählt im Binärcode

• der 74HC162 ist ein 4-Bit-Dezimalzähler

• der 74HC162 zählt im BCD-Code

Regeln

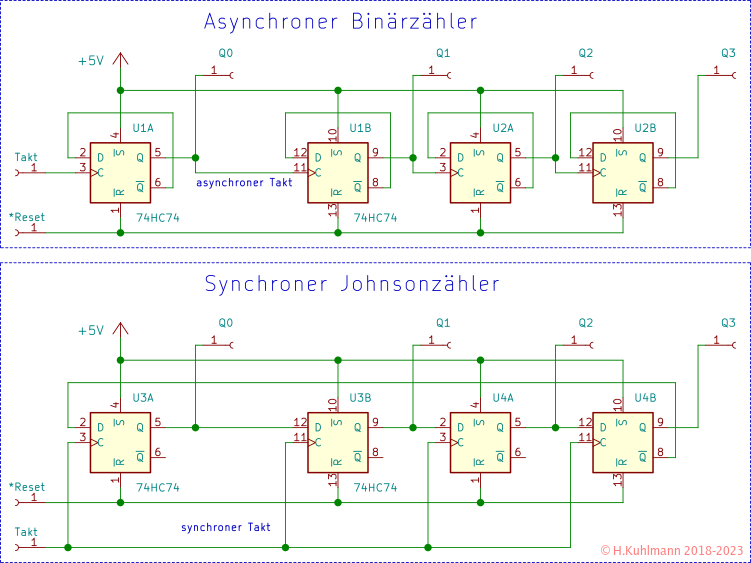
• Ein asynchroner Binärzähler besteht aus mehreren D-Registern, deren Eingang mit seinem invertierten Ausgang verbunden ist.

• Der Takteingang jeder Folgestufe ist mit dem Ausgang der Vorgängerstufe verbunden.

• Der externe Takt liegt am Eingang der ersten Stufe an.

• Diese Zähler sind asynchron, da jede Stufe einen anderen Takt hat.

• Jede Stufe halbiert die Frequenz der Vorgängerstufe.

• Die Taktfrequenz f wird

• von der 1. Stufe durch 2 geteilt,

• von der 2. Stufe durch 2*2=4 geteilt,

• von der 3. Stufe durch 2*2*2=8 geteilt,

• von der 4. Stufe durch 2*2*2*3=16 geteilt,

• von der 5. Stufe durch 2*2*2*2*2=32 geteilt,

• von der 10. Stufe durch 2¹⁰=2**10=1024 (zehnmal 2 mit sich selbst multiplizieren) geteilt,

• von der n. Stufe durch 2**n (n mal 2 mit sich selbst multiplizieren) geteilt.