Binär zählen
Die folgenden Schaltungen haben einen Takt-Eingang, der an einen entprellten Taster angeschlossen werden muss. Dazu wird besten das Takt-Modul verwendet.
Mit dem Reset-Taster wird die Schaltung in einen definierten Zustand gebracht: Er setzt alle Ausgänge auf 0.
Wir haben einige digitale Zähler untersucht.
- Der Johnson-Zähler hatte eine andere Codefolge als
- der Binärzähler.
Wir werden die Codefolgen genauer untersuchen und feststellen, dass der Binärzähler eine einfache Codefolge hat.
Binärzähler
Bits
Die einzelnen Stellen eines Binärzählers werden Bits genannt.
Der CD4040 ist z.B. ein 12 Bit-Zähler.
Wir haben uns den Binärzähler mit dem CD4040 angesehen.
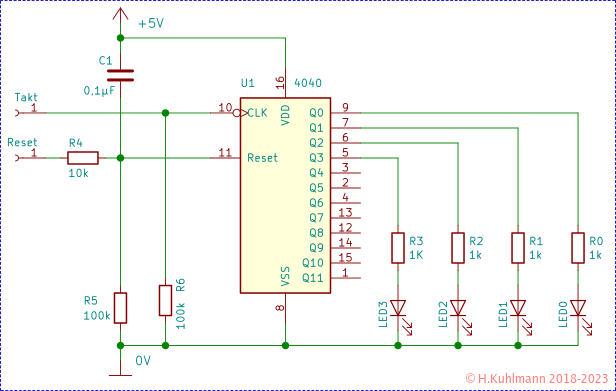
Im Praktikum Binärzähler haben wir die Zustände des Zählers notiert, den Binärzähler aber hauptsächlich als Frequenzteiler betrachtet.
| Takt | Q3 | Q2 | Q1 | Q0 |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 2 | 0 | 0 | 1 | 0 |
| 3 | 0 | 0 | 1 | 1 |
| 4 | 0 | 1 | 0 | 0 |
| 5 | 0 | 1 | 0 | 1 |
| 6 | 0 | 1 | 1 | 0 |
| 7 | 0 | 1 | 1 | 1 |
| 8 | 1 | 0 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 |
| 10 | 1 | 0 | 1 | 0 |
| 11 | 1 | 0 | 1 | 1 |
| 12 | 1 | 1 | 0 | 0 |
| 13 | 1 | 1 | 0 | 1 |
| 14 | 1 | 1 | 1 | 0 |
| 15 | 1 | 1 | 1 | 1 |
| 16 | 0 | 0 | 0 | 0 |
| 17 | 0 | 0 | 0 | 1 |
| 18 | 0 | 0 | 1 | 0 |
Tabelle 1: Folge der Zustände der ersten vier Ausgänge
Die Folge der Codes wiederholt sich nach sechzehn Takten. Den Codes können wir Zahlen zuordnen.
Wir brauchen nur noch eine Schaltung, die die zugeordneten Zahlen anzeigt ![]()
Sieben-Segment-Anzeige
Wir alle kennen LED-Anzeigen für Zahlen, z.B. von Uhren. Die Ziffern sind aus Segmenten einer 8 zusammengesetzt. Die 8 besteht aus sieben Segmenten. Deshalb werden diese Anzeigen auch Sieben-Segment-Anzeigen genannt.
Eine Sieben-Segment-Anzeige hat für jedes Segment eine LED, die von einer Digitalschaltung entsprechend angesteuert werden muss.

Eine Sieben-Segment-Anzeige enthält acht LEDs, sieben für die Elemente a-g und den Dezimalpunkt. Es gibt sie mit gemeinsamer Anode oder mit gemeinsamer Kathode. Wir verwenden eine mit gemeinsamer Kathode.
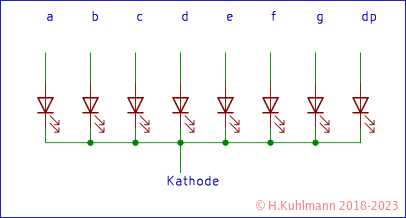
Es gibt einen Chip, der aus dem Binärcode eine Ziffer der Sieben-Segment-Anzeigen erzeugt, den 74HC4511.

An den Binärzähler von Bild 1 haben wir den 74HC4511 angeschlossen, der eine Sieben-Segment-Anzeige ansteuert.
Wir sehen die Codes an den Ausgängen Q0 bis Q3 auf den LEDs und die entsprechende Ziffer auf der Sieben-Segment-Anzeige.
Nach dem Reset zeigen die LED0 bis LED3 jeweils 0 an. Die Sieben-Segment-Anzeige zeigt die Ziffer 0.
Mit dem Taster lassen wir den Binärzähler weiterzählen. Die Codes von LED0 bis LED3 laufen entsprechend Tabelle 1 durch und die Sieben-Segment-Anzeige zeigt die zugeordnete Zahl.
Bei der 10 zeigt die Sieben-Segment-Anzeige nichts mehr an ![]()
Wie sollte sie auch. Die Anzeige kann nur eine Ziffer darstellen.
- Unsere Schaltung versagt völlig, wenn sie Zahlen über 9 darstellen soll.
- Wir könnten einen weiteren 74HC4511 einbauen, aber wo?
- An Q4 bis Q7. Wie aber, wenn der 74HC4511 schon bei Q0 bis Q3 versagt?
- Wir brauchen ein besseres Konzept.
BCD-Code
Die erstem zehn Codes des Binärzählers stellen nichts anderes als unsere Ziffern 0-9 dar.
0000 = 0 0001 = 1 0010 = 2 0011 = 3 0100 = 4 0101 = 5 0110 = 6 0111 = 7 1000 = 8 1001 = 9
Damit kann eine Dezimalstelle kodiert werden.
Es können auch Dezimalzahlen kodiert werden. Für jede Dezimalstelle wird einfach der obige Code eingetragen.
Für 27 tragen wir 0010 0111 ein. Für 1967 haben wir dann 0001 1001 0110 0111.
Wir haben die Lösung und nennen diesen Code BCD-Code, Binär Codierte Dezimalziffern.
Leider haben wir die Rechnung ohne den 4040 gemacht. Er zählt 0000 0001 .. 1000 1001 1010 ... Aber die 1010 ist nicht im BCD-Code. Der 4040 kennt den BCD-Code nicht.
Wir brauchen einen anderen Zähler-Chip, den 4518. Er kann zwei BCD-kodierte Stellen zählen.
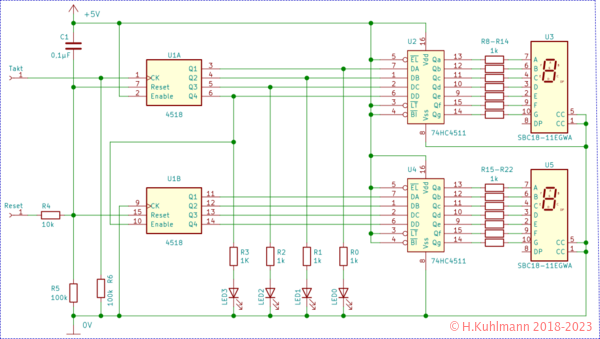
Unsere Schaltungen werden aufwendiger. Wir haben einen BCD-Zähler mit zwei Stellen. Er kann von 0 bis 99 zählen.
Der 4518 hat eigentlich zwei Takteingänge: CK und Enable.
- CK zählt bei einer ↑ Flanke, wenn Enable=1 ist,
- Enable bei einer ↓ Flanke, wenn CK=0 ist.
- U1B soll weiterzählen, wenn Q4 von U1A von 1 nach 0 geht, also mit der ↓ Flanke.
- Deshalb ist bei U1B CK=0 und Enable an Q4 von U1A angeschlossen.
Wir schauen auf die erste Stelle und vergleichen den von LDE1 bis LED4 angezeigten Code mit dem BCD-Code. Tatsächlich zählt Zähler von 0000 bis 1001 und beginnt dann wieder bei 0000.
Binärcode
Zählweise der Ausgänge
Die Ausgänge des 4518 werden mit Q1 bis Q4 bezeichnet.
Die Zählung beginnt bei 1.
- Diese Inkonsistenz ist zwar ärgerlich, aber so ist es nun einmal.
Der Zähler kann in vier Schritten bis sechzehn zählen. Nach dem sechzehnten Schritt beginnt der Zähler wieder bei Null. Jeder Zahl ist ein bestimmter Code zugeordnet. Wir können leicht erkennen, dass dem Ganzen eine gewisse Systematik zugrunde liegt.
| Gewicht | 8 | 4 | 2 | 1 |
| Zahl | Q4 | Q3 | Q2 | Q1 |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 2 | 0 | 0 | 1 | 0 |
| 3 | 0 | 0 | 1 | 1 |
| 4 | 0 | 1 | 0 | 0 |
| 5 | 0 | 1 | 0 | 1 |
| 6 | 0 | 1 | 1 | 0 |
| 7 | 0 | 1 | 1 | 1 |
| 8 | 1 | 0 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 |
| 10 | 1 | 0 | 1 | 0 |
| 11 | 1 | 0 | 1 | 1 |
| 12 | 1 | 1 | 0 | 0 |
| 13 | 1 | 1 | 0 | 1 |
| 14 | 1 | 1 | 1 | 0 |
| 15 | 1 | 1 | 1 | 1 |
Tabelle 2: Gewichteter Code der vier Ausgänge
In Tabelle 2 ist jedem Q ein bestimmtes Gewicht zugeordnet.
Mit den Gewichten der Qs können wird die Anzahl der Takte berechnen.
Wir addieren die Gewichte einer Zeile. Immer wenn eine 1 unter einem Q steht, wird das Gewicht addiert.
Wir fangen mit der Zahl 0 an, alle Qs sind 0. Wir brauchen nichts zu addieren ![]() das Ergebnis ist 0.
das Ergebnis ist 0.
In der Zeile 8 ist nur Q4=1. Wir erhalten 8.
In der Zeile 5 haben wir Q1=1 und Q3=1 und erhalten 1+4=5
Der Code sieht vereinfacht aus wie:
0000 = 0 0001 = 1 0010 = 2 0011 = 3 0100 = 4 0101 = 5 0110 = 6 0111 = 7 1000 = 8 1001 = 9 1010 = 10 1011 = 11 1100 = 12 1101 = 13 1110 = 14 1111 = 15
Dieser Code wird Binärcode genannt. Genau genommen handelt es sich um einen vierstelligen Binärcode.
Wir könnten diesen Codes einfach erweitern, indem wir am Anfang eine weitere Stelle einfügen. Dann hätten wir einen fünfstelligen Code.
Uns reichen die vier Stellen. Um den Binärcode in Zahlen umzuwandeln, benutzen wir die Tabelle. Mit der Zeit können wir sie auswendig.
Dezimal-Code
Wir schreiben unsere Zahlen auch in einem Code.
- Die Anzahl der Finger einer Hand wird mit 5 kodiert.
- Die Römer nahmen dafür V,
- Computer nehmen 0101,
- aber manchmal auch 5
- Für unsere 11
- nehmen Computer 1011
- oder B
- Wir verwenden den Dezimalcode mit den zehn Buchstaben 0 1 3 3 4 5 6 7 8 9
- Der Binärcode kennt nur die beiden Buchstaben 0 und 1
- Computer verwenden auch den Hex-Code mit den sechzehn Buchstaben 0, 1, ... 9, A, B, C, D, E, F
Die Kodierung ist zunächst ungewohnt, wird uns aber mit der Zeit vertraut.