Spannung, Strom, Polarität

Analyse des Stromkreises

In den vorangegangenen Praktika habe wir uns bereits mit den Begriffen Spannung und Strom vertraut gemacht:

Spannung bedeutet nichts anderes, als welche Möglichkeit, welche Potenz eine Batterie oder Spannungsquelle hat. Eine Spannungsquelle mit 1,5V kann z.B. keine LED zum Leuchten bringen. Dazu brauchen wir mindestens zwei Zellen oder 3V. Wir kennen sicher die 230V der Netzspannung und wissen auch, dass die Netzspannung einen Menschen (möglicherweise) töten kann. Wenn wir eine 1,5V Batterie anfassen, merken wir nichts.

Spannungen werden in Volt angegeben - geschrieben V.

Strom beschreibt die Energie, die wir einer Stromquelle entnehmen.

Strom wird in Ampere angegeben - geschrieben A. In der Elektronik arbeiten wir meistens mit tausendstel von Ampere, Milliampere, geschrieben mA.

Wir sprechen von Spannungsquelle und Stromquelle und meinen damit gleiche. Je nachdem, welche Brille wir aufsetzen, die rote Spannungsbrille oder die grüne Strombrille

Die Polarität einer Spannungsquelle bestimmt die Richtung, in der der Strom fließen kann. Sie wird durch die Symbole + und - dargestellt. Der Strom fließt immer von Plus nach Minus.

Zur Vorgehensweise:

Wir wissen, was Reihen- und Parallelschaltung sind und wie sie wirken. Wir haben bereits Spannungen und Ströme gemessen, einfache Berechnungen durchgeführt und diese mit Messungen überprüft. Das alles haben wir in Form von Regeln zusammengefasst.

An dieser Stelle werden wir zunächst die Reihen- und Parallelschaltung mehr von der theoretischen Seite betrachten.

Der Einsteiger sollte sich das Folgende ansehen und alles, was er nicht versteht, nicht so ernst nehmen.

Am Ende werden wir die Erkenntnisse in Regeln zusammenfassen.

Wenn wir uns länger mit Elektronik beschäftigen, werden wir mit der Zeit feststellen, dass es hilfreich ist, Formeln zu kennen.

UND, was viel wichtiger ist, wir werden durch unsere Praxis den Zusammenhang, den die Formeln beschreiben, immer besser verstehen.

Regeln

Die Regeln sollte sich jeder ansehen.

Bei Bedarf kann jederzeit auf dieses Praktikum zurückgegriffen werden.

Außerdem gibt es das Tool Ohm.

Reihenschaltung

Betrachten wir eine einfache Reihenschaltung mit zwei Widerständen und einer LED. Durch die drei Bauelemente fließt ein Strom. Er ist in allen drei Bauelementen gleich groß.

Strompfeile

Strompfeile werden in die Zuleitungen der Bauelemente eingezeichnet.

Sie zeigen von Puls nach Minus.

In Bild 1 haben wir den Strom durch Pfeile auf den Leitungen symbolisiert. Ströme werden mit I bezeichnet. In dem Schaltbild sind zwei Ströme eingetragen: I₁ und I₃. Wir wissen, dass in einer Reihenschaltung die Ströme gleich sind, also I₁=I₃.

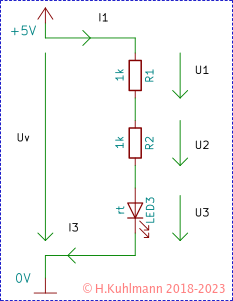
Spannungspfeile

Spannungspfeile werden neben die Bauelemente gezeichnet.

Sie zeigen von Puls nach Minus.

Spannungen fließen nicht. Sie liegen nur an. Deshalb werden sie als Pfeile neben den Bauelementen eingezeichnet.

In Bild 2 haben wir die drei Spannungen U₁, U₂ und U₃. Wir sagen, dass sie an den Widerständen R₁, R₃ und der LED3 abfallen. Wir haben noch eine weitere Spannung, U_v, die Spannung der Spannungsquelle mit 5V (oder die 4,5V der Batterie). Der Pfeil U_v ist interessant, weil er vom Plus zum Minus der Spannungsquelle zeigt. Wenn wir die Polarität einer Spannung kennen, zeichnen wir den Pfeil von Plus nach Minus ein. Die anderen Spannungspfeile zeichnen wir in die gleiche Richtung.

Fahren wir die Spannungspfeile einmal ab. Wir beginnen bei Plus und folgen den Pfeilen bis Minus. Wir fahren zuerst über U₁, dann U₂, schließlich U₃ und wir sind am Ziel.

Am einfachsten ist es aber mit U_v, wir gelangen unmittelbar von Plus nach Minus.

Zur Freude der Theoretiker können wir jetzt Mathematik betreiben:

Formel 1

   U_v = U₁ + U₂ + U₃

Was bringt uns das?

Die Summe der drei Spannungen entspricht der Versorgungsspannung.

Die Spannung an jedem der drei Bauelemente muss kleiner sein als die Versorgungsspannung.

Das Entscheidende ist aber, dass sich die Spannungen der Spannungspfeile addieren.

Treiben wir es auf die Spitze:

Wir fangen bei Plus an, fahren zuerst über U₁, U₂, U₃ und dann einfach weiter über U_v zurück nach Plus. Wir haben den ganzen Stromkreis abgefahren und haben nichts erreicht. Nun, das Nichts ist wichtig: es ist auch eine Spannung, nämlich 0V. In der Eile haben wir nicht notiert, dass wir den Pfeil U_v entgegen der Pfeilrichtung durchlaufen haben. Das ruft wieder die Mathematiker auf den Plan: U_v muss nicht addiert, sondern subtrahiert werden:

Formel 2

   U₁ + U₂ + U₃ - U_v = 0

Wer Formeln umstellen kann, sieht, dass sich Formel 2 aus Formel 1 ergibt.

Wichtig ist aber die Erkenntnis:

Wenn man in einem Stromkreis eine Schleife durchläuft, werden alle Spannungspfeile addiert. Wird jedoch ein Pfeil in entgegengesetzter Richtung durchlaufen, wird seine Spannung subtrahiert. Die Summe aller Spannungen ist 0.

Wir fahren andersherum:

Formel 3

   U_v - U₃ - U₂ - U₁ = 0

Formel 3 ergibt sich auch aus Formel 1.

Spannungen an LEDs

Besonders interessant ist die Spannung U₃ an der LED3.

Die Spannung an einer in Durchlassrichtung betriebenen LED kann als Faustregel angegeben werden. Sie hängt vom Typ und der Farbe der LED ab. Die Spannung an einer LED in Durchlassrichtung wird Flussspannung genannt.

Farbe	Flussspannung	Strom bei 3mm LEDs
rot	1,8V	20mA
gelb	2,0V	20mA
grün	2,2V	20mA
blau	3,0V	20mA
weiß	3,0V	20mA

Diese Spannungen sind nur Richtwerte. Je nach Exemplar kann die Flussspannung um ± 0,4V abweichen. Wenn eine LED glimmt, kann sie um 0,4V niedriger sein. Superhelle LEDs haben meistens eine höhere Flussspannung.

Wir haben eine rote LED verwendet und wissen, dass 1,8V an der LED abfallen. Die restliche Spannung muss offensichtlich an den beiden Widerständen abfallen. Uns reicht es, dass an beiden Widerständen zusammen 3,2V abfallen (bei einer Stromversorgung von 5V).

Was passiert, wenn wir den Widerstand R₂ entfernen und den Widerstand R₁ an die LED anschließen? An der LED fallen immer noch 1,8V ab. Dann müssen wohl die ganzen 3,2V am Widerstand R₁ abfallen. R₁ bedankt sich und liefert mehr Strom. Die LED3 leuchtet heller. Ausprobieren!

Die Theorie:

Formel 4

   U_v = U₁ + U₃

oder

Formel 5

   U₁ = U_v - U₃

Eines sollten wir uns merken: Wenn die Spannung an einem Widerstand höher wird, fließt mehr Strom.

Parallelschaltung

Die folgende Schaltung ist keine Parallelschaltung im eigentlichen Sinne. Die Widerstände sind parallel geschaltet. Dazu liegt die LED in Reihe.

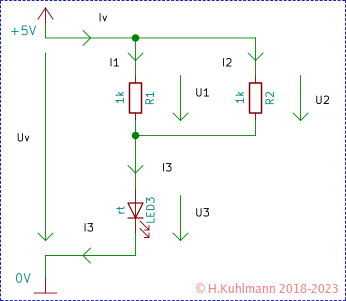
Mit Spannungen kennen wir uns schon ein wenig aus: Einmal im Kreis ergibt 0.

Fangen wir oben bei R₁ an, dann über R₂ wieder zurück zu R₁. Das war ein Kreis! Also

Formel 6

   U₁ - U₂ = 0

Gegen die Richtung von U₂, daher -U₂.

U₂ und U₁ sind gleich groß. Das ist doch offensichtlich. Womit nachgewiesen wurde, dass an der Theorie doch etwas dran ist.

Nun zu den Strömen. Wir betrachten Knoten, Punkte an denen mehrere Ströme zu- oder abfließen.

Am oberen Knoten (Punkt) kommt I_v an und die Ströme I₁ und I₂ fließen weiter. I_v teilt sich in I₁ und I₂ auf.

Formel 7

   I_v = I₁ + I₂

Betrachten wir den unteren Punkt. Wir haben:

Formel 8

   I₁ + I₂ = I₃

Aus den Formeln 7 und 8 ergibt sich

Formel 9

   I_v = I₃

Das war uns aber ohne die Formeln klar.

Die Sache mit der Null

Alle Strompfeile eines Knotens werden addiert. Die in den Knoten hineinfließenden Ströme werden mit einem Pluszeichen versehen, Ströme, die aus dem Knoten herausfließen, werden mit einem Minuszeichen versehen. Die Summe ist Null.

Formel 10

   I_v - I₁ - I₂ = 0
   I₁ + I₂ - I₃ = 0

Strom, Spannung und Widerstand

Wir haben oben schon gesehen, dass mehr Strom fließt, wenn die Spannung an einem Widerstand größer wird. Wir wissen auch, dass mehr Strom fließt, wenn der Widerstand kleiner wird.

Diesen einfachen Zusammenhang können wir noch etwas präziser fassen: Zwischen der Spannung am Widerstand, dem Strom durch den Widerstand und dem Wert des Widerstands gibt es einen eindeutigen Zusammenhang, der als Ohmsches Gesetz bezeichnet wird.

Wir fassen es in drei Formeln zusammen:

Formel 11

   U = I * R

Formel 12

   I = U / R

Formel 13

   R = U / I

Wenn also zwei der drei Größen bekannt sind, können wir die dritte berechnen.

Kennen wir den Strom I und den Widerstand R, so können wir mit Formel 11 die Spannung U berechnen.

Kennen wir die Spannung U und den Widerstand R, berechnen wir den Strom I mit Formel 12.

Kennen wir die Spannung U und den Strom I, verwenden wir Formel 13, um den Widerstand R zu berechnen.

Das Ohmsche Gesetz haben wir in den Praktika [Le-Spannungen-messen.niki[Spannungen messen]] und [Le-Stroeme-messen.niki[Ströme messen]] angewendet, um indirekt den Strom zu bestimmen, der durch einen Widerstand fließt.

Das Tool Ohm unterstützt uns bei der Berechnung.

Maßeinheiten

Wir messen

	Spannungen in Volt	V
	Ströme in Ampere	A
	Widerstände in Ohm	Ω

In den obigen Formeln werden Ströme in Ampere, Spannungen in Volt und Widerstände in Ohm eingesetzt.

Für Elektroniker ist das nicht sehr praktisch. Durch einen Widerstand von 1kΩ an 5V fließen

I = U / R
I = 5V / 1kΩ
I = 5V / 1000Ω
I = 0,005A
I = 5mA

Das können wir vereinfachen:

Spannung	Strom	Widerstand
U	I	R
V	A	Ω
V	mA	kΩ
V	µA	MΩ

1A	1000mA	10000µA
0,001A	1mA	1000µA
0,000001A	0,001mA	1µA
1MΩ	1000kΩ	1000000Ω
0,001MΩ	1kΩ	1000Ω
0,000001Ω	0,001kΩ	1Ω

Das Tool Ohm kann natürlich auch mit Maßeinheiten arbeiten.

Vorwiderstand für LEDs

Im Praktikum Arbeiten mit Kennlinien wird eine weitere Methode vorgestellt, den Vorwiderstand von LEDs zu bestimmen.

Jetzt haben wir alles, was wir brauchen, um den Vorwiderstand von LEDs zu bestimmen.

Bild 4: Reihenschaltung von Widerstand und LED

Wir kennen die Versorgungsspannung (4,5V Batterie oder 5V Netzgerät).

Wir kennen die Spannung an einer LED (1,8V für rot oder 3,0V für blau usw.).

Wir wissen, dass normale (3mm) LEDs mit maximal 20mA betrieben werden.

Die Theorie sagt:

Die Spannung am Widerstand ist die Versorgungsspannung abzüglich der LED-Spannung

         U₁ = U_v - U_led
         U₁ = 5V - 1,8V
         U₁ = 3,2V

Der Widerstand ist die Spannung dividiert durch den Strom.

         R₁ = U₁ / I
         R₁ = 3,2V / 20mA
         R₁ = 0,16kΩ

Wir erinnern uns: kΩ und mA gehören zusammen, 0,16kΩ sind 160Ω.

Die Praxis

In der E24-Reihe gibt es keinen 160Ω-Widerstand.

Es gibt nur 150Ω oder 220Ω.

Wir müssen den 220Ω Widerstand nehmen, weil bei 150Ω der Strom durch die LED zu groß würde.

Stimmt's? nachrechnen, nachmessen.
Welcher Strom fließt durch einen 150Ω Widerstand, welcher durch einen mit 220Ω?

Die 150Ω könnten eine LED zerstören.
Den Unterschied in der Helligkeit einer LED bei 150Ω und 220Ω können wir kaum sehen.
Versuch macht klug!

Der Vorwiderstand für LEDs kann mit dem Tool LED berechnet werden.

Tools

Für diejenigen, denen die Anwendung des Ohmschen Gesetzes zu schwierig ist, gibt es das Tool Ohm: Berechnung von Strom, Spannung und Widerstand.

Die Berechnung des Vorwiderstands auch für mehrere LEDs unterstützt das Tool LED.

Regeln

Ein Spannungspfeil wird parallel zu einem Bauelement eingetragen. Der Spannungspfeil bekommt einen eindeutigen Namen. Am besten den Namen des Bauteils (U₁ für R₁).

Spannungspfeile werden so eingezeichnet, dass sie von Plus nach Minus zeigen.

Wenn die Polarität (noch) nicht bekannt ist, wird eine Richtung gewählt.

Falls die Spannung einen negativen Wert hat, liegt sie mit umgekehrter Polarität an.

Wenn Bauelemente hintereinander (in Reihe) geschaltet sind, verteilt sich die Spannung auf die Bauelemente.

Ein Stromkreis muss geschlossen sein, aber nicht unbedingt die Spannungsquelle enthalten.

Beim Durchfahren eines Stromkreises lässt sich die zugehörige Gleichung (Formel) leicht aufstellen.

Die Spannungen aller Spannungspfeile werden eingetragen:

Wird ein Spannungspfeil in Pfeilrichtung durchfahren, wird die Spannung mit + eingetragen.

Wird ein Spannungspfeil gegen dir Pfeilrichtung durchfahren, wird die Spannung mit - eingetragen.

Am Ende wird =0 eingetragen.

Wenn mehrere Leitungen miteinander verbunden sind, wird die Verbindung im Schaltbild durch einen Punkt dargestellt. Wir nennen die Verbindung von Leitungen einen Knoten.

Ein Strompfeil wird in die Leitung eines Bauelements eingezeichnet. Der Strompfeil erhält einen eindeutigen Namen. Am besten den Namen des Bauteils (I₁ für R₁).

Strompfeile werden so eingezeichnet, dass der Strom von Plus nach Minus fließt.

Wenn die Richtung (noch) nicht bekannt ist, wird eine Richtung gewählt.

Falls der Strom einen negativen Wert hat, zeigt der Pfeil in entgegengesetzte Richtung.

Der Strom, der in einen Widerstand (mit seinen zwei Anschlüssen) hineinfließt, ist genauso groß wie der Strom, der herausfließt. Dasselbe gilt für eine LED oder eine Diode. Dies gilt nicht für Bauelemente mit mehr als zwei Anschlüssen.

Bei parallel liegenden Bauelementen teilt sich der hineinfließende Strom auf die parallelen Bauelemente auf.

Bei mehreren Leitungen an einem Knoten ist die Summe der zufließenden Ströme gleich der Summe der abfließenden Ströme.

Die Gleichung (Formel) für einen Knoten kann leicht aufgestellt werden:

Die Ströme aller Strompfeile werden eingetragen:

Zeigt der Pfeil auf den Knoten, wird der Strom mit + eingetragen.

Zeigt der Pfeil vom Knoten weg, wird der Strom mit - eingetragen.

Am Ende wird =0 eingetragen.

Wenn die Spannung an einem Widerstand größer wird, fließt ein größerer Strom.

Bei kleinerem Widerstand und gleicher Spannung fließt ein größerer Strom.

Wenn kein Strom durch einen Widerstand fließt, ist die Spannung an diesem Widerstand 0V.

Mithilfe des Ohmschen Gesetzes können wir Spannung, Strom oder Widerstand berechnen, wenn wir die beiden anderen Größen kennen.

   U = I * R

   I = U / R

   R = U / I

V, A und Ω gehören zusammen.

V, mA und kΩ gehören zusammen.

Es geht auch ohne =0

Gleichung für einen Stromkreis:

Wir schreiben in die Mitte einer Zeile ein = .

Für jeden Spannungspfeil, den wir in Pfeilrichtung durchlaufen, tragen wir die Spannung rechts vom Gleichheitszeichen mit + ein.

Für jeden Spannungspfeil, den wir in Pfeilrichtung durchlaufen, tragen wir die Spannung links vom Gleichheitszeichen mit + ein.

Gleichung für einen Knotenpunkt:

Wir schreiben in die Mitte einer Zeile ein = .

Für jeden Strompfeil, der in Richtung des Knotens zeigt, tragen wir den Strom rechts vom Gleichheitszeichen mit + ein.

Für jeden Strompfeil, der aus dem Knoten herausführt, tragen wir den Strom links vom Gleichheitszeichen mit + ein.

Wir werden die Regeln in Komplexe Schaltungen anwenden.

Strom messen

Das Messen von Strömen ist aufwendig.

Um Ströme messen zu können, müssen die Leitungen, deren Ströme gemessen werden sollen, aufgetrennt werden.

Das Messen von Strömen kann zur Beschädigung des Messgeräts und der Schaltung führen.

Wenn möglich, sollten Ströme indirekt über Spannungen an Widerständen bestimmt werden.

    I = U / R

Wir betrachten die Reihenschaltung von Widerstand und LED unter dem Aspekt der Messung des Stroms durch die LED.

Wir brauchen nur die Spannung am Widerstand R₁ zu messen und berechnen den Strom über I_led = U₁ / R₁. Das ist möglich, weil der Strom I₁ durch R₁ der gleiche ist wie I_led.

Das Tool Ohm erledigt die Berechnung.