Parallele Widerstände und LEDs
Wir experimentieren mit einigen Schaltungen, bauen sie auf und notieren die Ergebnisse.
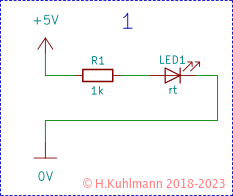
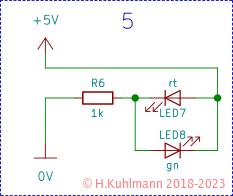
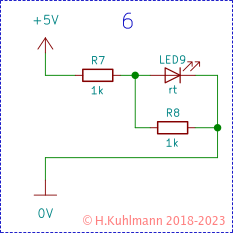
Ergebnisse der Schaltungen 1 bis 6
Ergebnis: Die LED leuchtet.
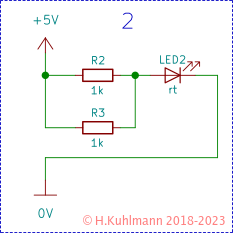
Ergebnis: Die LED leuchtet heller.
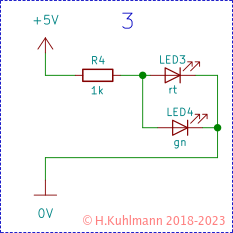
Ergebnis: Die LEDs leuchten dunkler. Die grüne LED ist wesentlich dunkler als die rote.
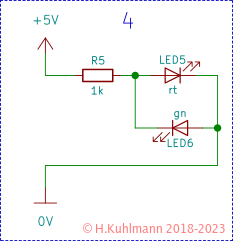
Ergebnis: Nur die grüne LED leuchtet mit normaler Helligkeit.
Ergebnis: Nur die rote LED leuchtet mit normaler Helligkeit.
Die LED leuchtet nur noch schwach.
Zusammenfassung
In Schaltung 2 summiert sich offensichtlich der Strom durch die Widerstände R2 und R3 in der LED2. Da die beiden Widerstände gleich groß sind, fließt durch die LED der doppelte Strom.
In Schaltung 3 müsste sich dementsprechend der Strom durch die beiden LEDs zu gleichen Teilen aufteilen. Das ist aber nicht der Fall, weil die rote LED besser leitet und der grünen Strom entzieht. Wegen dieser Eigenschaft von LEDs sollten sie niemals unmittelbar parallel geschaltet werden.
In Schaltung 6 haben wir einen ähnlichen Fallt wie in Schaltung 5, hier entzieht der Widerstand R8 der LED9 Strom.
Die Schaltungen 4 und 5 sind für uns von besonderem Interesse. Eigentlich sind beide Schaltungen gleich.
Sie sind jedoch umgekehrt an die Stromversorgung angeschlossen. Nur die LED, die in Durchlassrichtung betrieben wird, leuchtet, leitet also. Die LED in Sperrrichtung stört überhaupt nicht. Wir sagen, die LEDs sind antiparallel geschaltet.
Parallelschaltung von Widerständen
Die beiden obigen Schaltungen 1. und 2. unterscheiden sich nur dadurch, dass ein oder zwei Widerstände parallel geschaltet sind.
Die LED leuchtet jedoch heller, wenn zwei Widerstände parallel geschaltet sind.
Die Wirkung der beiden parallel geschalteten Widerstände von 1kΩ ist die gleiche wie die eines Widerstandes von 500Ω (0,5kΩ).
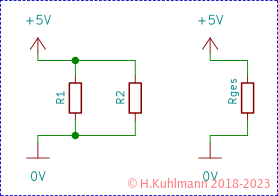
Auf der linken Seite sind zwei Widerstände R1 und R2 parallel geschaltet. Auf der rechten Seite werden diese beiden Widerstände durch einen Gesamtwiderstand Rges ersetzt.
Der Gesamtwiderstand Rges kann berechnet werden:
R1 * R2
Rges = ———————
R1 + R2
Einfacher ist es, wenn zwei gleiche Widerstände R parallel geschaltet sind,
Rges = R / 2
Wenn mehrere, sagen wir N, gleiche Widerstände R parallel geschaltet sind, ist
Rges = R / N
Der Gesamtwiderstand von parallel geschalteten gleichen Widerständen ist einfach der Widerstandswert geteilt durch die Anzahl.
Regeln
- Werden Widerstände parallel geschaltet, erhöht sich der Gesamtstrom durch die parallelen Widerstände.
- LEDs dürfen in Durchlassrichtung nicht parallel geschaltet werden.
-
LEDs können antiparallel geschaltet werden.
Je nach Polarität der Versorgungsspannung leuchtet dann diejenige, die in Durchlassrichtung betrieben wird.
- Wird ein Widerstand parallel zu einer LED geschaltet, fließt durch den parallelen Widerstand ein Teil des Stroms ab.
- Zwei in parallel geschaltete Widerstände haben einen Gesamtwiderstand Rges, der mit folgender Formel berechnet werden kann:
R1 * R2
Rges = ———————
R1 + R2
- Bei mehreren parallel geschalteten Widerständen ist die Berechnung des Gesamtwiderstands aufwendiger:
1 1 1 1
———— = —— + —— + —— + ....
Rges R1 R2 R3
- Der Gesamtwiderstand parallel geschalteter Widerstände ist immer keiner als der kleinste Einzelwiderstand.
- Werden Widerstände parallel vor eine LED geschaltet, wird die LED heller.
- Wegen der Empfindlichkeit unserer Augen nehmen wir diesen Effekt erst wahr, wenn der sich Gesamtwiderstand mindestens halbiert wird, wir z.B. zwei gleiche Widerstände parallel geschalten.
Arbeiten mit dem Taschenrechner
Taschenrechner
- Unter Arbeiten mit dem Taschenrechner, werden einfache Anleitungen gegeben.
- Taschenrechner für Elektroniker stellt eine kleine Auswahl vor.
- Interessant ist der HiPER Scientific Calculator für Android .
- Die Formeln für die Berechnung des Gesamtwiderstands für Parallelschaltung sind komplizierter als für Reihenschaltung.
- Sie enthalten Brüche
- Ein Taschenrechner kann uns helfen,
- aber er kann uns auch reinlegen.
Beispiel: Zwei parallele Widerstände
Wir vollen den Gesamtwiderstand von R1=100Ω parallel zu R2=200Ω berechnen.
Wir nehmen die Formel
R1 * R2
Rges = ———————
R1 + R2
und rechnen
100 x 200 / 100 + 200 =
Der Taschenrechner zeigt 400 an.
Das ist offensichtlich falsch, weil der Gesamtwiderstand kleiner als der kleinste Einzelwiderstand sein muss.
Wir haben vergessen dem Taschenrechner mitzuteilen, dass er die 100 + 200 erst addieren muss und dann dividieren:
100 x 200 / ( 100 + 200 ) =
Der Taschenrechner zeigt den korrekten Wert 66,67 an.
- Die Klammern sind wichtig!
Die Tasten des Taschenrechners sind rot dargestellt.
Beispiel: Drei parallele Widerstände
Wir vollen den Gesamtwiderstand von R1=100Ω parallel zu R2=200Ω und R3=150Ω berechnen.
Wir nehmen die Formel
1 1 1 1
———— = —— + —— + ——
Rges R1 R2 R3
Die Brüche lassen die Berechnung kompliziert erscheinen 
- aber mit dem Taschenrechner ist es ganz einfach.
- Er hat nämlich die Funktions-Taste 1/x oder X-1.
Damit können wir die 1 / R1 usw. leicht berechnen:
( 100 1/x + 200 1/x + 150 1/x ) 1/x =
Das ergibt 46,15...
- Die Klammern sind wichtig.
Berechnung von Parallelschaltungen zu Fuss
- Für zwei oder mehr parallele Widerstände
zuerst +, dann
den Widerstandswert eingeben und
schließlich 1/x
) 1/x =
Übungen
| Parallele Widerstände | ergibt |
| 300Ω parallel zu 300Ω und 300Ω | 100Ω |
| 200Ω parallel zu 200Ω | 100Ω |
| 1kΩ parallel zu 100Ω | 90,90Ω |
| 1kΩ parallel zu 100Ω und 2kΩ | 86.956Ω |
Ω, kΩ und MΩ
- Alle Werte werden in Ω angegeben.
-
kΩ müssen in Ω umgerechnet werden,
d.h. mit 1000 multipliziert werden.
- Mit dem richtigen Taschenrechner können wir uns die die Umrechnung der Präfixe (k und M) sparen: der Taschenrechner erledigt das für uns. Ein Rezept gibt es unter Arbeiten mit dem Taschenrechner.