Taschenrechner für Elektroniker
Wir betrachten die folgenden Rechner:
Die Auswahl der Taschenrechner ist zufällig und keineswegs vollständig.

- Gut geeignet
- Beherrscht keine Präfixe
Den REBELL SC2040 gibt es bei Reichelt für etwa 6 €.

- Bestens geeignet.
Den CASIO fx-85DE X gibt es bei Reichelt für etwa 26,95 €.
Andere Varianten der fx-Serie sind
fx-991DE X
fx-87DE X
fx-82DE X

- Gut geeignet
- Beherrscht keine Präfixe
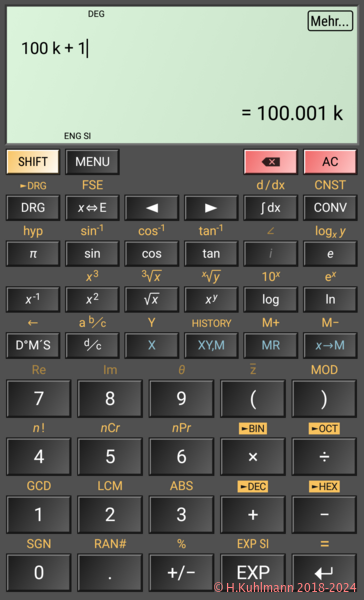
- Bestens geeignet.
Empfehlung
- Der HiPER Scientific Calculator für Android
- und der CASIO fx-85DE X sind für Elektroniker bestens geeignet.
- Sie haben eine x-1-Taste und
- die Funktionen ln und ex.
- Sie beherrschen Klammern ( ) und
- Präfixe wie µ k oder M
- bei der Eingabe wie auch bei der Anzeige.
HiPER einstellen
- Menu -> Modus
- Ausdrücke
- Reell
- Shift -> x ⇔ E
- Techn. + Präfix

- Dieser Taschenrechner ist nur bedingt geeignet.
- Es fehlen 1/x, ln, ex,
- die technische Darstellung und
- präfixe.
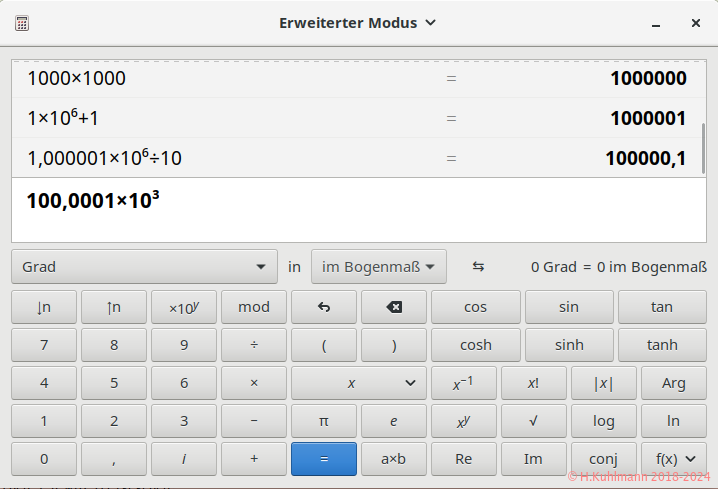
- Dieser Taschenrechner ist gut geeignet.
- Die Funktion ex kann über e und xy berechnet werden.
- Unterstützt keine Präfixe.
- Der KDE-Taschenrechner ist nicht sehr hilfreich.
Viele der angebotenen Funktionen benötigen wir für die praktische Arbeit nicht.
Wir brauchen unbedingt
- Klammern ( ) und
- 1/x bzw. x-1
- technisches (ingenieurwissenschaftliches) Zahlenformat
- In der Regel muss der Rechner auf den ENG-Modus gestellt werden.
- Am besten wäre es, wenn angehängte Einheiten wie µ, m, k oder M angezeigt werden.
- Diese angehängten Einheiten werden als Präfixe bezeichnet.
- Eine Anzeige mit 10-6, 10-3, 103 oder 106, also Dreiersprünge in den Zehnerpotenzen, ist auch brauchbar.
Fazit
-
 Der HiPER Scientific Calculator für Android ist sehr gut geeignet.
Der HiPER Scientific Calculator für Android ist sehr gut geeignet.
- Er beherrscht Präfixe.
- Umstellung der Anzeige mit FSE.
- Eingabe von Präfixen mit EXP SI.
-
 Der CASIO fx-85DE X ist sehr gut geeignet.
Der CASIO fx-85DE X ist sehr gut geeignet.
- Er beherrscht Präfixe.
- Umstellung der Anzeige mit ENG.
- Präfixe müssen im Setup aktiviert sein (SHIFT MENU 4 1).
- Eingabe von Präfixen mit OPTN 3.
- Der RealCalc für Android ist gut geeignet.
- Mit FSE wird das Zahlenformat umgeschaltet.
- Der Taschenrechner von Linux ist gut geeignet.
- Einstellungen -> Zahlenformat -> Ingenieurwissenschaftlich
- Der Taschenrechner von Windows ist nicht so gut geeignet, weil er
- keine 1/x-Taste bietet und
- kein technisches Zahlenformat beherrscht.
Präfixe
Präfixe sind Vorsätze für Maßeinheiten. Sie werden hinter die Zahl und vor die Maßeinheit eines Wertes geschrieben.
- Beispiel: 1000 Ω = 1 kΩ mit dem Präfix k.
- Präfixe werden auch als Dezimalpräfixe oder Einheitenvorsätze bezeichnet.
Zehnerpotenzen und Präfixe
Wir kennen die Schreibweise mit Präfixen wie µ, m, k, M usw.
Im technischen Bereich ist die Schreibweise mit Zehnerpotenzen üblich.
Man schreibt z. B. statt:
| 1001 | 1.001*10 3 |
| 0.00012 | 1.2*10 -4 |
| 1.001 | 1.001*10 0 |
| 1 | 10 0 |
In der Elektronik ist diese Schreibweise nützlich, weil wir nicht viele Nullen vor und nach dem Komma schreiben und zählen müssen.
- Die Zahl über der 10 gibt nur an, um wie viele Stellen das Komma verschoben werden muss,
- bei positiven Zahlen nach rechts,
- bei negativen Zahlen nach links.
Diese Schreibweise ist für die Elektronik nicht ganz befriedigend, weil wir mit den Präfixen wie µ, m, k, M usw. lieber Sprünge von 3 in den Zehnerpotenzen hätten.
- Aber am liebsten haben wir die Präfixe selbst.
Damit sind also Präfixe einfache Faktoren:
| Präfix | Name | Faktor | 10er-Potenz |
| p | piko | 1*10 -12 | |
| n | nano | 1*10 -9 | |
| µ | mikro | 0.000001 | 1*10 -6 |
| m | milli | 0.001 | 1*10 -3 |
| k | kilo | 1000 | 1*10 3 |
| M | Mega | 1000000 | 1*10 6 |
| G | Giga | 1*10 9 |
Zehnerpotenzen auf Taschenrechnern
Darstellung von Zehnerpotenzen
- Die meisten Taschenrechner stellen Zehnerpotenzen heute in der Form 1.1*106 dar.
- Einige verwenden jedoch 1.1e6
Eingabe von Zehnerpotenzen
- Vor der Eingabe einer Zehnerpotenz muss die Taste
- EXP
- x10y oder
- EXP SI oder OPTN 3 (Eingabe mit Präfix)
betätigt werden.
Zehnerpotenzen
Wir lieben Präfixe,
aber sie behindern uns beim Rechnen.
Zum Beispiel wollen wir die Zeitkonstante τ = R * C mit C=2,2 nF und R=100 kΩ berechnen.
Dazu müssen wir die Faktoren für die Präfixe einsetzen:
n -> 10-9 k -> 103
Also
2.210-9 * 100103
Das Ergebnis ist:
0.00022 oder
2.2*10 -4 oder
220µ
- Ein Taschenrechner, der Präfixe beherrscht, nimmt uns die Umrechnung ab.
Beispiel
Parallele Widerstände
Der Gesamtwiderstand zweier paralleler Widerstände R1=20 Ω und R2=30 Ω wird mit
Formel 1
R1 * R2
Rges = ———————
R1 + R2
berechnet.
Brüche wie in der obigen Formel lassen sich nicht direkt in den Taschenrechner eingeben. Wir müssen die ⸓-Taste benutzen.
Wenn wir die obige Formel blauäugig einfach eingeben:
20 x 30 ⸓ 20 + 30 =
erhalten wir fälschlicherweise 60.
Wir müssen dem Taschenrechner mitteilen, dass die beiden letzten Werte vor der Division noch addiert werden müssen. Das geschieht mit Klammern:
20 x 30 ⸓ ( 20 + 30 ) =
Eigentlich müssten wir auch die erste Multiplikation in Klammern setzen:
( 20 x 30 ) ⸓ ( 20 + 30 ) =
- Diese Formel erfordert die mehrfache Eingabe von Werten.
- Dies kann zu Fehlern führen.
Alternative
Die parallelen Widerstände können auch mit
Formel 2
1 1 1 ———— = —— + —— Rges R1 R2
berechnet werden.
Das sieht noch komplizierter aus als Formel 1.
Auf dem Taschenrechner ist es aber einfacher als im ersten Fall, wenn wir die Funktion x-1 oder 1/x verwenden:
( 20 x-1 + 30 x-1 ) x-1 =
Das Ergebnis ist dasselbe wie bei der ersten Formel.
- Wir mussten weniger Tasten betätigen und
- die Werte nur einmal eingeben.
Der größte Vorteil ist aber, dass wir mit dieser Formel auch den
- Gesamtwiderstand von mehr als zwei parallelen Widerständen berechnen können:
Formel 3
1 1 1 1 ———— = —— + —— + —— + .... Rges R1 R2 R3
Rezepte
- In Arbeiten mit dem Taschenrechner werden Rezepte für die Arbeit mit
- und dem fx-85DE X von CASIO
beschrieben.