Differenzieller Widerstand
Wir kommen später zurück
Wir machen eine Reihe von Klimmzügen, um zu zeigen, dass eine LED einen "eingebauten" Vorwiderstand hat.
Diesen Widerstand nennen wir hochtrabend differenziellen Widerstand.
Im Praktikum Arbeiten mit Kennlinien haben wir festgestellt, dass eine blaue LED ohne Vorwiderstand an 3 V betrieben werden kann.
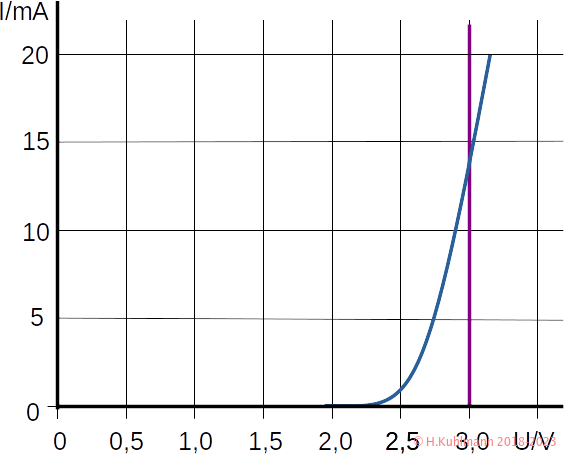
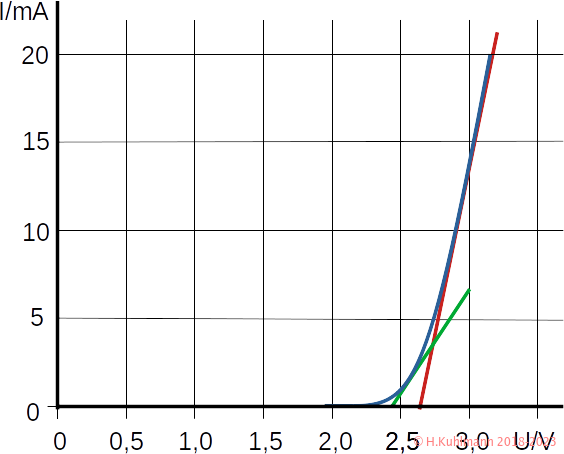
In Bild 1 wird eine blaue LED ohne Vorwiderstand an 3 V betrieben.
Die violette Kennlinie ist die einer 3 V-Spannungsquelle ohne Widerstand (0 Ω).
- Sie schneidet die Kennlinie der blauen LED bei (3 V; 13 mA).
Wir können also eine blaue LED ohne Vorwiderstand an 3 V betreiben.
- Damit brechen wir unsere eigenen Regeln.
- Nein, die blaue LED hat einen eingebauten Vorwiderstand.
Kennlinie eines Akkus mit Diode und Widerstand
Wir betrachten die Ladeschaltung eines Akkumulators.
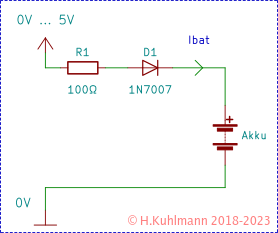
Die Ladeschaltung ist einfach. Wir haben eine Spannungsquelle, über die der Akku geladen werden soll. Der Widerstand R1 begrenzt den Ladestrom und der Gleichrichter D1 verhindert, dass der Akku entladen wird, wenn die Spannung unter der des Akkus liegt.
Die Spannungsquelle können wir zwischen Uv = 0 V und 5 V einstellen. Der Akku besteht aus zwei Nickel-Cadmium-Zellen mit je 1,2 V, also Ub = 2,4 V.
Wir wollen die Kennlinie der Ladeschaltung bestimmen.
Wenn die Spannung Uv kleiner als die Akkuspannung Ub = 2,4 V ist, sperrt die Diode. Erst wenn die Spannung an dem Gleichrichter größer als seine Flussspannung ist, fließt ein Strom in den Akku.
Ein Gleichrichter 1N4007 hat eine Flussspannung von etwa 0,7 V. Ab Uv = 2,4 V + 0,7 V = 3,1 V fließt ein Strom. Bei Uv = 5 V fällt dann am Widerstand R1 die Spannung U1 = 5 V - 2,4 V - 0,7 V = 1,9 V ab, d. h., es fließt ein Strom Ibat = 1,9 V / 100 Ω = 19 mA.
Wir haben alles, um die Kennlinie unserer Ladeschaltung zu zeichnen.
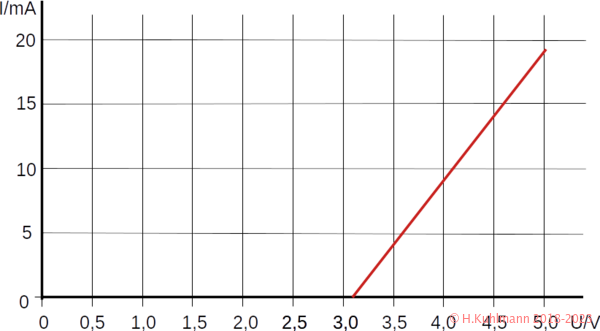
Diese Kennlinie ist relativ einfach zu berechnen und zu zeichnen. Sie besteht nur aus einer Geraden.
Wenn wir die Kennlinie betrachten, sieht sie fast so aus wie die Kennlinie einer Diode oder Z-Diode. Sie ist nur nicht gekrümmt.
Betrachten wir nun die Kennlinie der blauen LED in Bild 1. Wenn wir den uns interessierenden Teil der Kennlinie um 10 mA durch eine Gerade ersetzen, haben wir damit die LED sehr einfach beschrieben.
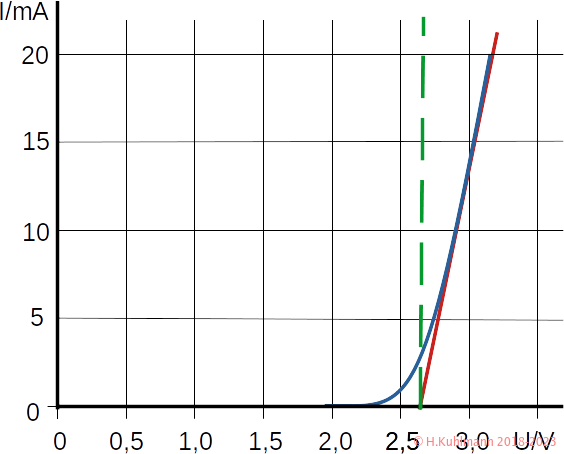
Die rote Kennlinie entspricht der unserer Ladeschaltung. Die Akkuspannung und der Widerstand sind jedoch unterschiedlich.
Die Spannung lässt sich leicht ablesen: Bei einem Strom von 0 beträgt sie 2,65 V. Den Widerstand müssen wir noch berechnen. Bei 3,2 V ist der Strom 20 mA und wir erhalten:
R = ( 3,2V - 2,65V ) / 20mA R = 0,55V / 20mA R = 27,5Ω
Wir können unsere blaue LED durch eine Diode mit einer konstanten Flussspannung von 2,65 V in Reihe mit einem Widerstand von 27,5 Ω beschreiben.
- Konstante Flussspannung heißt, dass die Flussspannung nicht vom Strom abhängt. Dies entspricht der grün gestrichelten Kennlinie in Bild 4.
- Na ja, fast.
Widerstand der LED
Wir haben den eingebauten Vorwiderstand der blauen LED bestimmt:
Eine blaue LED hat
- eine (konstante) Flussspannung von 2,65 V und
- einen eingebauten Vorwiderstand von 27,5 Ω.
Bei einem Strom von 2 mA liegen wir ziemlich daneben.
- Unsere Beschreibung gilt nur für Ströme von 5 mA bis 20 mA.
- Wir haben die einfache Beschreibung damit erkauft, dass sie nur in einem bestimmten Bereich gültig ist.
Versuchen wir die gleiche Prozedur noch einmal für Ströme um 2 mA.
In Bild 5 haben wir die Kennlinie bei 2 mA durch eine Gerade beschrieben.
- Das sieht nicht besonders gut aus. Wir liegen fast überall daneben.
- Aber zwischen 1 mA und 3 mA passt sie ganz gut.
- Die (konstante) Flussspannung ist hier 2,45 V und der Widerstand bei 85 Ω.
Zusammenfassung
- Wir haben eine LED durch eine Gerade beschrieben.
- Diese Gerade entspricht einem Widerstand
- bei einer (konstanten) Flussspannung.
- Diese Gerade berührt die Kennlinie der LED an einer Stelle, sie tangiert sie.
- Diese Gerade beschreibt die LED nur in einem mehr oder weniger kleinen Bereich.
- Um den Widerstand zu berechnen, haben wir die Änderung der Spannung der LED und die Änderung des Stroms durch die LED verwendet, um den Ersatzwiderstand zu berechnen.
- Wir haben die Differenzen der Spannung und des Stroms verwendet.
- Dieser Ersatzwiderstand wird als differenzieller Widerstand bezeichnet.
- Genau genommen beschreiben wir die gekrümmte Kennlinie einer LED durch eine Menge von differenziellen Widerständen, die in bestimmten Bereichen gültig sind.
- Diese Bereiche hängen von der Genauigkeit ab, mit der wir die gekrümmte Kennlinie beschreiben wollen.
- Die Geraden beschreiben die Kennlinie tatsächlich nur genau an dem Punkt, an dem sie die Kennlinie tangieren.
- Dieses Verfahren können wir auf alle gekrümmten Kennlinien anwenden.
Tangente
Eine Tangente ist eine Gerade, die eine Kurve in einem bestimmten Punkt berührt, nicht durchschneidet.
So geht's
Wir haben eine gekrümmte Kennlinie.
- Wir interessieren uns für einen bestimmten Bereich der Kennlinie.
- Wir zeichnen mit dem Lineal eine Gerade in den Bereich der Kennlinie, der uns interessiert.
- Die Gerade soll die Kennlinie nur in einem Punkt tangieren.
- Wir erhalten die (konstante) Flussspannung Uf für den Strom I=0, indem wir die Gerade bis zu I=0 verlängern und die Spannung ablesen.
- Wir wählen einen zweiten Punkt auf der Geraden (U2, I2).
- Unser erster Punkt ist U1=Uf und I1=0.
- Wir berechnen den differenziellen Widerstand:
Rd = (U2 - U1) / (I2 - I1) Rd = (U2 - Uf) / I2
Regeln
- Je steiler die Gerade ist, desto kleiner ist der differenzielle Widerstand.
- Je flacher die Gerade ist, desto größer ist der differenzielle Widerstand.
- Wenn die Gerade mit der Spannung fällt, ist der differenzielle Widerstand negativ.