Prinzip eines elektronischen Würfels
Normalerweise wird die 3 auf einem Würfel diagonal dargestellt.
Wir erlauben uns die künstlerische Freiheit, sie horizontal darzustellen.
Diese Darstellung ist viel logischer.
Ein elektronischer Würfel ist im Prinzip einfach aufgebaut. Ein Zähler wird von einem Taktgeber angetrieben. Der Takt kann mit einem Taster ausgeschaltet werden. Die Zustände des Zählers werden durch eine Logik auf die sechs LEDs des Würfels abgebildet.
Der Zähler zählt so schnell, dass der Zählerstand beim Anhalten zufällig ist.
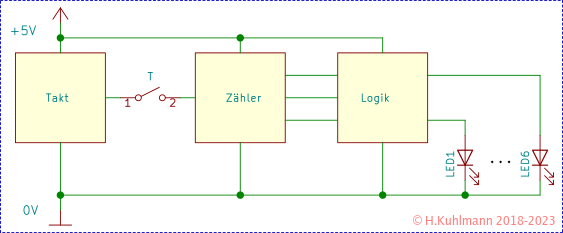
Die Komponenten Taktgenerator, Zähler und Logik sind bekannt und werden hier angewendet.
Der Taktgenerator ist ein NE555 mit etwa 10000 Hz. Die Widerstände und der Kondensator lassen sich leicht mit dem Tool Astabiler Timer 555 berechnen: R1=510 kΩ, R2=470 kΩ, C1=1 nF. Wir nehmen R1=R2=100 kΩ und C1=1 nF und erhalten 4,8 kHz.
Als Zähler könnten wir einen Binärzähler verwenden. Binärzähler zählen bis 2, 4 oder 8. Der dreistufige Johnson-Zähler dagegen hat wie ein Würfel sechs Zustände. Wir versuchen, den elektronischen Würfel mit einem Johnson-Zähler zu bauen.
Die Logik des Würfels
Die Logik scheint nicht so einfach zu sein.
Ein Würfel hat sieben Punkte, die wir mit LEDs darstellen.
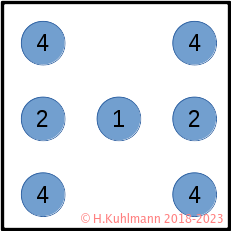
Bild 2 zeigt einen Würfel, dessen Punkte bewertet sind.
Die einzelnen Punkte des Würfels können wir zuordnen.
| Würfel | Punkte |
| 1 | 1 |
| 2 | 2 |
| 3 | 2 + 1 |
| 4 | 4 |
| 5 | 4 + 1 |
| 6 | 4 + 2 |
Tabelle 1: Zuordnung der Punkte des Würfels
Die Tabelle 1 zeigt die Berechnung der Dezimalzahl aus dem Binärcode.
| Takt | Q4 | Q3 | Q2 | Q1 |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 2 | 0 | 0 | 1 | 0 |
| 3 | 0 | 0 | 1 | 1 |
| 4 | 0 | 1 | 0 | 0 |
| 5 | 0 | 1 | 0 | 1 |
| 6 | 0 | 1 | 1 | 0 |
| 7 | 0 | 1 | 1 | 1 |
Tabelle 2: Binärcode der ersten acht Zahlen
Q4 wird nicht benötigt und Q1 bis Q3 können den LEDs zugeordnet werden:
| Q1 | 1 LED |
| Q2 | 2 LED |
| Q3 | 4 LED |
Tabelle 4: Zuordnung der LEDs
Logik berechnen
Wenn wir einfach die Codes des Binärzählers verwenden, können wir die Logik für die LEDs berechnen.
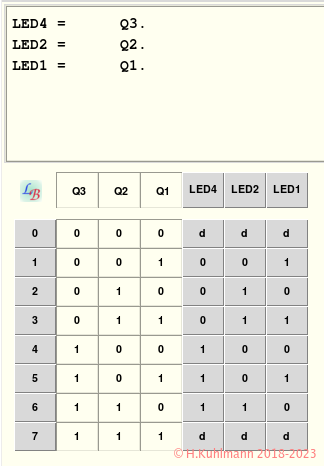
Bild 3: Binäre Codierung des Würfels
Die nicht im Würfel enthaltenen Zahlen 0 und 7 haben wir ausgeblendet. Einfacher kann die Logik nicht sein.
Leider zählt der Johnson-Zähler nicht binär. Die binären 2 und 5 kommen im Code des Johnson-Zählers nicht vor. Außerdem ist die Zuordnung der Zahlen anders. Die Zuordnung interessiert uns beim Würfel nicht. Es macht nichts, wenn der Würfel nicht in der richtigen Reihenfolge zählt. Er zählt so schnell, dass wir es nicht merken. Wichtig ist aber, dass alle Zahlen gleich oft vorkommen. In unserer Schaltung kommen alle Zahlen einmal pro Durchlauf vor.
- Wir können die Reihenfolge der Zahlen überprüfen, indem wir anstelle des Timers 555 den Takt mit einem Taster erzeugen.
Wir vertauschen in der Logik einfach die 2 mit 7 und die 5 mit 0.
Die Logik ist dann:
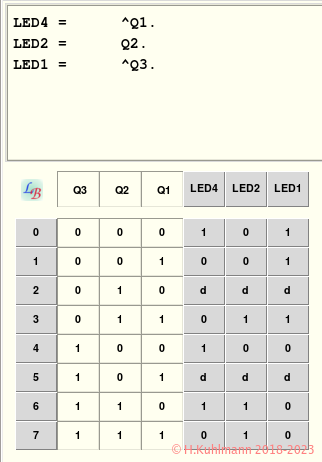
Bild 4: Codierung des Würfels mit Johnson-Zähler
Wie zählt ein Würfel
Na klar: 1, 2, 3, 4, 5, 6
Oder?
Wenn wir einen Würfel rollen, zählt er 1, 2, 6, 5, 1 oder 1, 4, 6, 3, 1 oder ...
Meist kippt der Würfel noch ...
Die Schaltung aufbauen
Bauen wir die Schaltung auf. Die zwei LEDs für die 2 und die vier für die 4 können wir jeweils mit einem Vorwiderstand von 1 kΩ verbinden. Bei 5 V können wir auch zwei rote LEDs in Reihe schalten. Das Programm LED liefert einen Vorwiderstand von 430 Ω. Die LED für die 1 muss mit 1 kΩ auskommen.
Den Timer haben wir bereits berechnet.
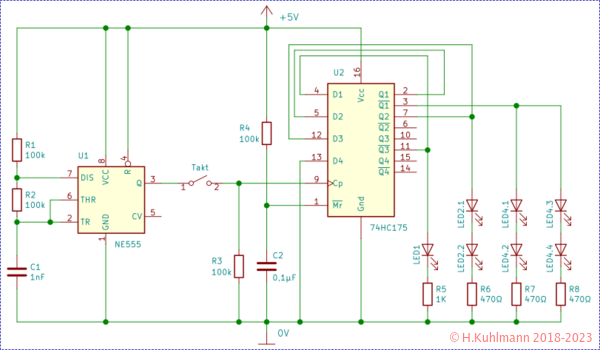
Der Ausgang des Taktgenerators wird über einen Taster mit dem Takteingang des 74HC175 verbunden. Dieser zählt, bis der Taster losgelassen wird. Die LEDs an den Ausgängen zeigen dann den zufällig getroffenen Zustand an.
Der Widerstand R3 sorgt dafür, dass der Takteingang nie offen ist.
Welche Logik hat der Würfel?
Es gibt eine Reihe von Schaltungen. Sie verwenden immer einen Zähler, der von einem Taktgenerator angetrieben wird. Die LEDs sind meist über eine Logik mit dem Zähler verbunden.
Unsere Schaltung kommt ohne diese Logik aus. Allerdings haben wir die Anzeige des Würfels angepasst. Normalerweise wird die 3 diagonal angezeigt. Wir stellen sie horizontal oder wie in Bild 6 vertikal dar. Dadurch wird der Würfel logisch. Bei unserem Würfel ist 3=1+2, meist wird 3=1+4/2 genommen 
Fertiger Bausatz
Natürlich kann ein elektronischer Würfel mit einem einzigen IC mit acht Beinen gebaut werden. Das ist dann ein Prozessor, der entsprechend programmiert wird. Meist wird er in einem Bausatz mit einer Platine fertig programmiert geliefert.
- Aber was haben wir dann gelernt, außer Löten?
- Wie wäre es dagegen, unseren elektronischen Würfel auf einer Lochrasterplatine aufzubauen?