Herleitung für den Widlar-Stromspiegel

Wir betrachten die Schaltung des Widlar-Stromspiegels:

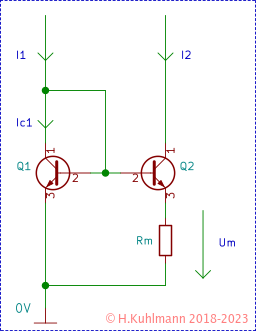
Wir gehen von der bekannten Beziehung zwischen Kollektorstrom und Basis-Emitter-Spannung aus:

Ic = Io exp( Ube / Ut )

mit

I_o Sperrsättigungsstrom (hängt vom Transistor ab)

U_t Thermische Spannung (kT/q) ~ 26mV bei Raumtemperatur

Dann gilt:

Ube  = Ut ln( Ic  / Io )
Ube1 = Ut ln( Ic1 / Io ) ~ Ut ln( I1 / Io )    (1)
Ube2 = Ut ln( Ic2 / Io ) = Ut ln( I2 / Io )    (2)

Die Basisströme I_b1 und I_b2 sind im Vergleich zum Kollektorstrom I_c1 sehr klein, I_b1 + I_b2 << I_c. Sie wurden in (1) vernachlässigt, d.h. I₁ ~ I_c1.

Die Transistoren Q1 und Q2 haben die gleichen Parameter, d.h. I_o ist gleich.

Und wegen

ln(x) - ln(y) = ln(x/y)

ist

Ube1 - Ube2 = Ut ln( I1 / I2 )
Um          = Ut ln( I1 / I2 )

Damit konnte Widlar den Widerstand R_m berechnen, um den Ausgangsstrom einzustellen:

Um        =   Ut * ln( I1 / I2 )
Iout * Rm =   Ut * ln( I1 / I2 )
Rm        = ( Ut * ln( I1 / I2 ) ) * I2
Ut        = 26mV

Genauer gesagt konnte Widlar aus dem Eingangsstrom I₁ des Stromspiegels den für den Ausgangsstrom I₂ erforderlichen Widerstand R_m berechnen.

Betrachten wir den normalen Stromspiegel:

Dann ist I₁ = I₂ und I₁ / I₂ = 1. Da ln ( I₁ / I₂ ) = ln (1) = 0, ist R_m = 0.

Richtig, für den normalen Stromspiegel gibt es kein R_m.