Wie funktioniert MP3?

MP3 ist ein Verfahren zur komprimierten Speicherung von Audiosignalen. Die Tonsignale werden sozusagen in Notenschrift übersetzt. Zusätzlich werden für den Menschen unhörbare Töne in der Aufnahme zusammengefasst oder weggelassen.

Noch einfacher beschreibt es Musiker können MP3

Schlagworte

Im Internet werden zur Erklärung von MP3 immer wieder Schlagworte anstelle einer grundlegenden Erklärung verwendet, z.B.

• psychoakustische Effekte

• Quantisierung

• Huffman-Kodierung

Diese Verfahren können jedoch erst nach Durchführung des grundlegenden Verfahrens, der Fourier-Transformation, angewendet werden.

Die Fourier-Transformation beruht auf Prinzipien, die wir alle kennen: Noten.

Im Folgenden wird die Fourier-Transformation einfach, nicht simpel, beschrieben.

Eine Erklärung der Methoden hinter MP3,

• die bei den Grundlagen beginnt,

• die auf Mathematik verzichtet und

• dennoch das Prinzip der zugrundeliegenden mathematischen Verfahren vermittelt.

Wussten Sie,

• dass bei MP3 die wesentliche Datenreduktion nicht auf Zippen beruht?

• dass die Aufzeichnung von Musik auf CD und MP3 auf völlig unterschiedlichen Prinzipien beruht?

• dass Musiknoten eine Spektraldarstellung von Musik sind?

• dass MP3 eine Spektraldarstellung - im Prinzip Noten - von Musik aufzeichnet?

• dass eine Drehorgel sozusagen ein mechanischer MP3-Player ist?

• dass MP3 Kopfarbeit maschinisiert: automatisiert (modern: digitalisiert)?

Musik aufzeichnen und wiedergeben

Jeder von uns nutzt sie: Musik aus dem Internet.

Einige von uns wissen, dass die Wiedergabequalität an die von CDs heranreicht, aber nur etwa ein Zehntel der Datenmenge benötigt wird.

Dahinter steckt die Erfahrung und Praxis vieler Musiker. Es steckt aber auch viel Mathematik dahinter.

Hier wird versucht, auf Mathematik, Formeln, Berechnungen usw. zu verzichten, und dennoch ein Verständnis für das Verfahren zu vermitteln.

Andererseits ist dieses Verfahren ein gutes Beispiel dafür, wie Techniken, die wir alle beherrschen, automatisiert werden.

Wir gehen von unserer Fähigkeit aus, Musik "aufzuzeichnen", und betrachten, wie wir im Laufe der Zeit neue Verfahren entwickelt haben.

Musik memorieren

Schon damals, als die Menschen noch keine Schrift kannten, konnten sie sich Musik merken. Das können wir alle. Wir hören ein Musikstück und speichern es in unserem Gedächtnis. Manche Stücke können wir mit unserer Stimme oder mit Instrumenten wiedergeben.

Natürlich können nur wenige von uns umfangreiche Musikstücke aus dem Gedächtnis mit Stimme und Instrumenten wiedergeben. Manche Virtuosen bewundern und verehren wir für ihre Fähigkeiten.

Interessant ist in diesem Zusammenhang, dass wir leicht erkennen, ob ein Musikstück auf einem anderen Instrument oder von einem anderen Interpreten gespielt wird. Es ist für uns selbstverständlich, dass jede Interpretation anders klingt und sich in Nuancen unterscheidet.

Musikkonserven

Heutzutage hören wir meistens Musik aus der Konserve. Bis auf den letzten Ton klingt alles gleich. Trotzdem oder gerade wegen der Unterschiede genießen wir Live-Auftritte.

Musik aufschreiben

Wir kennen ein weiteres Verfahren, Musik aufzuzeichnen. Es ist Jahrhunderte alt. Musik wird in Noten aufgeschrieben. Einige von uns können Musik nach Noten spielen. Oft spielen mehrere von uns gleichzeitig.

Nur wenige von uns sind in der Lage, ein Musikstück, das wir gehört haben, in Noten zu übertragen. Niemand kann so schnell schreiben. Diejenigen, die es können, merken sich ein Musikstück und schreiben es dann auf.

Mozarts Diebstahl

Das Miserere von Gregorio Allegri durfte bis 1770 nur zu Ostern in der Sixtinischen Kapelle aufgeführt werden. Das Abschreiben der Noten wurde vom Papst bei Strafe verboten.

Der vierzehnjährige Mozart hörte das Stück nur einmal und schrieb es dann aus dem Gedächtnis auf.

Technologie der Noten

Wir betrachten die Notation von Musik aus technischer Sicht und beschreiben sie mit ihren Begriffen.

Spektraldarstellung

Einige von uns haben den Begriff Spektrum oder Spektraldarstellung schon einmal gehört. Die meisten können nicht viel damit anfangen.

Nun, Noten sind die Spektraldarstellung von Musik.

Es gibt auch die Zeitdarstellung von Musik.

Zeitdarstellung von Musik ist ein hochtrabender Begriff für etwas Triviales, nämlich Musik, die gespielt wird, die wir hören. Die Musik läuft mit der Zeit ab.

Jemand, der ein Musikstück nach Noten spielt, wandelt die Spektraldarstellung eines Musikstücks in eine Zeitdarstellung um.

Transformation

Betrachten wir den Vorgang der Transformation von Noten in die Zeitdarstellung etwas genauer.

Noten haben eine bestimmte Tonhöhe (Linie) und eine bestimmte Dauer (ganze, halbe ...). Der Musiker spielt die Note entsprechend.

Meistens müssen mehrere Noten gleichzeitig gespielt werden (Akkorde auf dem Instrument).

Es ist auch angegeben, wie laut man spielen soll.

Aber das ist noch nicht alles. Es wird angegeben, auf welchem Instrument das Musikstück gespielt werden soll. Oft sind mehrere oder sogar viele Instrumente beteiligt.

Fassen wir das Ganze einmal systematisch zusammen. In den Noten steht:

• die Tonhöhe (Frequenz)

• die Dauer

• die Lautstärke, die Dynamik (Amplitude)

• den Satz von Instrumenten (Klängen)

Aus diesen Angaben kann das notierte Musikstück rekonstruiert, d.h. gespielt werden.

Musik im Zeitbereich

Natürlich kennen wir alle Musik im Zeitbereich, wir hören Musik. An dieser Stelle wollen wir etwas tiefer in die Materie einsteigen.

Moderne Mediaplayer liefern Bilder, die die aktuelle Musik widerspiegeln. Manchmal sieht das so

oder

so ähnlich aus. Meistens zappeln die Bilder im Rhythmus der Musik. Sie geben die Schwingungen der Musik wieder.

Diese Schwingungen sind kompliziert und für uns unverständlich. Um eine Vorstellung zu bekommen, schauen wir uns ein einfaches Instrument an, die Blockflöte. Sie hat einen klaren Klang. Die Schwingungen, die eine Blockflöte erzeugt, sind einfach.

Die Schwingungen einer Blockflöte sehen so aus:

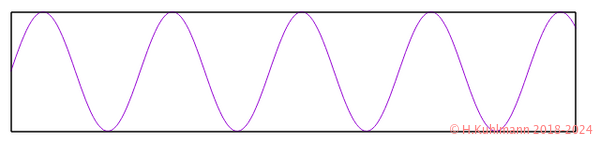
Die Flöte spielt a¹

Eine Oktave tiefer:

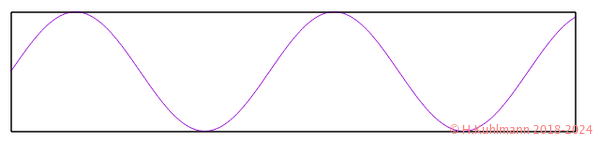
Die Flöte spielt a

Relativ einfach.

Noten

Wir haben Noten in einer Weise betrachtet, die dem üblichen Gebrauch teilweise widerspricht. Meistens wird Musik komponiert und dann nach Noten gespielt.

Dabei wird nicht nur die Abfolge der Noten festgelegt, sondern auch, welche Instrumente und Töne (Tasten, Saiten) gleichzeitig gespielt werden sollen.

Musik mechanisieren

Klänge konstruieren

Vor einigen Jahrhunderten kamen kluge Musiker auf die Idee, ein Instrument zu bauen, das die Klänge aller - vieler - Instrumente erzeugen sollte.

Es waren riesige Maschinen, die wir heute noch bewundern und hören können - Orgeln. Eine Orgel besteht aus vielen Pfeifen. Jede einzelne Pfeife erzeugt einen Ton, der dem einer Blockflöte ähnelt. Eine Orgel erzeugt ihren Klang, indem sie für jeden gespielten Ton eine ganze Reihe von Orgelpfeifen gleichzeitig erklingen lässt.

Ein bestimmter Klang wird synthetisch erzeugt, indem Pfeifen zusammen ertönen.

Musik automatisch wiedergeben

Wir kennen kleine Musikautomaten - Spieluhren. Ein Federwerk treibt eine Walze an, auf der kleine Stifte angeordnet sind. Jeder Stift stößt eine Zunge an, die in einer bestimmten Tonhöhe klingt.

Jede Zunge entspricht einer Tonhöhe, einer Linie auf dem Notenblatt. Jeder Stift entspricht einer Note auf dieser Linie.

Solche Musikautomaten wurden um 1900 in verschiedenen Formen entwickelt. Beliebt sind bis heute Glockenspiele.

Technisch gesehen wird die Musik nicht mehr in Noten, sondern mechanisch dargestellt. Die Automaten unterscheiden sich im Klang des zugrunde liegenden Tonerzeuger, den Zungen oder Glocken.

Drehorgeln verbinden die mechanische Darstellung des Spektrums der Musik mit der Synthese von Klängen.

Die Drehorgel

Eine Drehorgel ist die mechanische Variante eines MP3-Players.

Das Spektrum eines Musikstücks wird mechanisch mit einer Walze und Stiften dargestellt. Eine Reihe von Tönen (Pfeifen) wird gleichzeitig zum Klingen gebracht. Auf diese Weise werden Tonfolgen aber auch Klänge erzeugt.

In der Drehorgel wird die Transformation von Musik aus dem Spektral- in den Zeitbereich mechanisiert.

Musik aufnehmen

Wir betrachten hier, wie Musik aufgenommen und wiedergegeben werden kann.

Menschen merken sich Musik und spielen sie ab.

Aber können wir das automatisieren?

Musik im Spektralbereich aufnehmen

Die Technik, Musik aufzunehmen und automatisch wiederzugeben, ist ziemlich ausgereift. Mit der Drehorgel wurde beides mechanisiert. Ein wesentlicher Schritt zur vollautomatischen Aufnahme und Wiedergabe von Musik fehlt noch. Die Transformation vom Zeit- in den Spektralbereich. Im Klartext: Es fehlt ein Gerät, das die Stifte der Orgelwalze erzeugt.

Aufnahme von Musik im Zeitbereich

Die zuvor beschriebene automatische Musikwiedergabe basiert auf der Wiedergaben von Noten. Technisch gesehen beruht sie auf einer Transformation vom Spektral- in den Zeitbereich. Sie hat den Nachteil, dass sie nur einen begrenzten Bereich von Klängen erzeugen kann. Die Klänge sind durch die zugrunde liegende Tonerzeugung vorgegeben.

Wir wenden uns nun der Musikwiedergabe zu, die sich nur im Zeitbereich bewegt und die Klänge nicht einschränkt.

Das klingt sehr technisch, aber wir kennen diese Technik. Wir werden uns mit Schallplatten beschäftigen.

Unter "Musik im Zeitbereich" haben wir uns mit den zugrundeliegenden Schwingungen beschäftigt. Zu Beginn des 20. Jahrhunderts gelang es, diese Schwingungen mechanisch aufzuzeichnen und wiederzugeben. Inzwischen werden mechanische Schwingungen in elektrische umgewandelt und über Lautsprecher wieder in mechanische zurückverwandelt.

Musik im Zeitbereich digital aufzeichnen

Mit der CD begann das digitale Zeitalter.

Technisch gesehen ist die CD eine Aufzeichnung im Zeitbereich. Die Schwingungen werden in eine Folge digitaler Werte umgewandelt, auf die CD gebrannt und mit dem CD-Player über Lautsprecher wieder in Schwingungen zurückverwandelt. Eine Transformation in den oder aus dem Spektralbereich findet nicht statt.

Der technische Fortschritt bestand darin, dass sehr schnelle und sehr genaue Wandler zur Verfügung standen, die die "analoge" Schwingung in eine Folge digitaler Werte umwandeln konnten. Und natürlich die CD als digitales Speichermedium.

Auf dem Computer gibt es Dateien, die Musik im Zeitbereich in digitaler Form speichern. Es sind Dateien im WAV-Format.

Musik transformieren

Wir haben festgestellt, dass für die Aufnahme von Musik im Spektralbereich weniger Daten benötigt werden. Andererseits ist die automatische Transformation vom Spektral- in den Zeitbereich zwar möglich, aber nur unzureichend, da der Bereich der Klänge sehr begrenzt ist.

Wie die automatische Transformation vom Zeitbereich in den Spektralbereich erfolgen soll, können wir uns nicht einmal vorstellen.

Wir konzentrieren uns zunächst auf die Transformation vom Spektralbereich in den Zeitbereich.

Wir benötigen

• die Tonhöhe (Frequenz),

• die Dauer,

• die Lautstärke, Dynamik (Amplitude) und

• einen Satz von Instrumenten (Klängen).

Die Instrumente sind das größte Problem. Jedes Instrument hat seinen eigenen charakteristischen Klang. Es ist unmöglich, alle denkbaren Instrumente vorzusehen.

Die Orgelbauer haben es uns vorgemacht. Alles, was wir brauchen, sind Pfeifen, die wir für jeden Klang entsprechend kombinieren. Jede wird mit der richtigen Lautstärke und Dauer gespielt. Mit einem Computer könnten wir es schaffen.

Und es gelingt uns. Moderne elektronische Orgeln, Keyboards sind das Ergebnis.

Aber jetzt stehen wir vor dem viel größeren Problem, die Noten für die Pfeifen zu finden. Wir müssen die Musik aus dem Zeitbereich in den Spektralbereich transformieren, und da haben wir bisher außer dem Verweis auf Genies wie Mozart keinen Fingerzeig bekommen.

Der französische Mathematiker Fourier hat um 1820 ein Verfahren entwickelt, mit dem eine Transformation vom dem Zeitbereich in den Spektralbereich und umgekehrt wieder zurück möglich ist. Fouriers Transformation basiert auf einem Satz von Pfeifen.

Er benutzte relativ einfache mathematische Funktionen, die den Schwingungen der Pfeifen entsprechen. Es sind Sinus- und Kosinus-Funktionen.

Zu Ehren von Fourier werden diese Transformationen Fourier-Transformationen genannt.

Leider sind die Fourier-Transformationen mathematisch so kompliziert, dass Fourier es in seinem ganzen Leben nicht geschafft hätte, ein einfaches Lied in den Spektralbereich zu transformieren.

Fourier-Transformation

Die Fourier-Transformation ist ein mathematisches Verfahren, das auf Prinzipien beruht, die wir in der Musik anwenden:

• Wir wir spielen Musik im Zeitbereich

• Noten sind das Spektrum der Musik

• Noten spielen,

• die Transformation vom Spektral- in den Zeitbereich

• Noten aufschreiben.

• die Transformation vom dem Zeit- in den Spektralbereich

Noten- und Fourier-Spektrum

In diesem Abschnitt werden wir die Spektraldarstellung durch Noten und Fourier betrachten. Anschließend gehen wir auf den Zusammenhang zwischen Spektral- und Zeitdarstellung ein.

Für die Darstellung eines Fourier-Spektrums ist die Notenschrift zu kompliziert. So werden z.B. den Notenlinien Halbtöne mit Vorzeichen zugeordnet. Die Tastatur eines Klaviers ist jedoch eine gute Darstellung, um auch Halbtöne zuordnen zu können.

Urheber von Bild 5: Phillip Kuhrt (Original by Sergey Pushkin) Wikipedia

Bild 5 zeigt, dass ein Klavier mehrere Oktaven hat. Eine Oktave umfasst acht Töne. Aber die Musiker schummeln: Das Klavier hat zwölf Töne in einer Oktave, nämlich zusätzlich vier Halbtöne. Ein Klavier hat auch zwölf Saiten pro Oktave.

Technisch gesehen, müssen für das Spektrum mehrere Oktaven mit zwölf Tonhöhen dargestellt werden.

Das Spektrum wird nicht wie Noten mit gleichzeitig gespielten Tönen, untereinander, sondern nebeneinander dargestellt. Bild 6 zeigt drei Oktaven mit je zwölf Tönen.

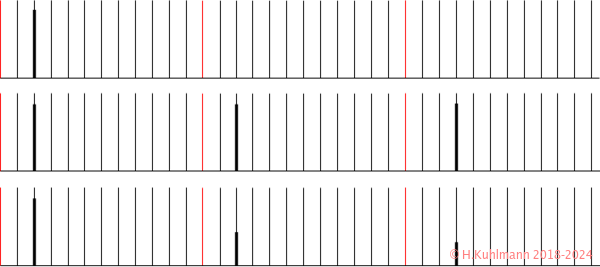
Das obere Spektrum in Bild 7 enthält nur einen Ton. Das mittlere enthält drei Töne, die jeweils eine Oktave höher liegen. Die Länge des Striches gibt an, wie laut der Ton gespielt werden soll. Im unteren Spektrum sind die Töne der höheren Oktaven leiser.

Sehen wir uns die entsprechenden Zeitdarstellungen an.

Eine Flöte spielt a

Das obere Spektrum erzeugt nur einen Ton mit dem Klang einer Blockflöte.

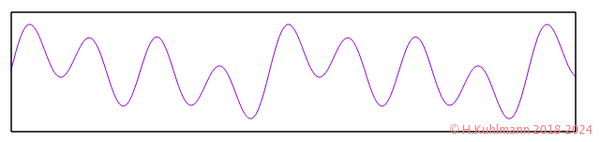
Drei Flöten spielen a, a¹ und a²

Der Ton des mittleren Spektrums klingt nicht wie eine Blockflöte, sondern wie drei Blockflöten, die jeweils eine Oktave höher gespielt werden.

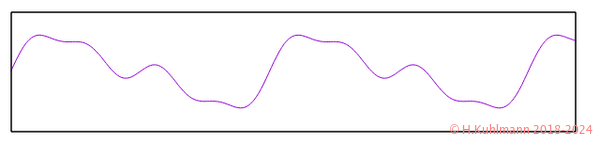
Drei Flöten spielen a, a¹ und a² jeweils leiser

Das untere Spektrum klingt wieder anders. Allerdings ist es schwierig, die Flöten jeweils leiser zu spielen.

Diese drei Spektren zeigen, wie wir mit den Tönen von Flöten Klänge erzeugen können. Wir empfinden sie als schön: harmonische Töne.

Schauen wir uns Klänge an, die weniger harmonisch sind.

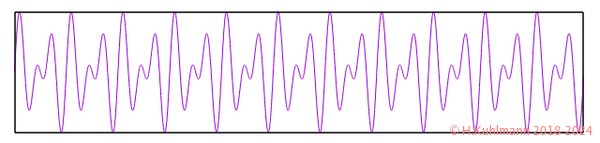
Konsonanter Klang

Die Zeitdarstellung dieser Töne sieht kompliziert aus.

Das Spektrum besteht nur aus zwei Tönen, die aber in der derselben Oktave liegen.

Eine Dissonanz besteht aus zwei Tönen, die aber zu nahe beieinander liegen.

In der Zeitdarstellung:

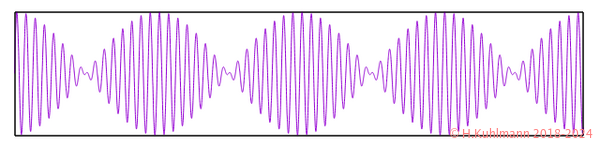
Die Zeitdarstellung dieses dissonanten Klangs sieht besser aus als die des konsonanten in Bild 11. Wir sehen eine Schwingung von Schwingungen. Techniker nennen das Schwebung.

Dissonanter Klang

Wir mögen dieses Wimmern nicht.

Die Beispiele zeigen, dass mit einfachen Spektren komplexe Klänge im Zeitbereich beschrieben werden können.

Fourier-Transformation von Musik

Heute haben wir leistungsfähige Rechenknechte, die Computer, die eine Fourier-Transformation mit Links durchführen. Aber sie brauchen die zu transformierende Musik in digitaler Form. Diese steht uns seit dem Zeitalter der CD zur Verfügung. Interessant ist in diesem Zusammenhang, dass die Transformation vom Zeitbereich in den Spektralbereich wesentlich aufwendiger ist als zurück in den Zeitbereich. Ein Computer erledigt die Wandlung in den Spektralbereich, das Ergebnis wird gespeichert und mehrfach kopiert. Das Abspielen übernehmen einfache Maschinen - unsere Player.

Ein schönes Beispiel stammt aus der Wikipedia:

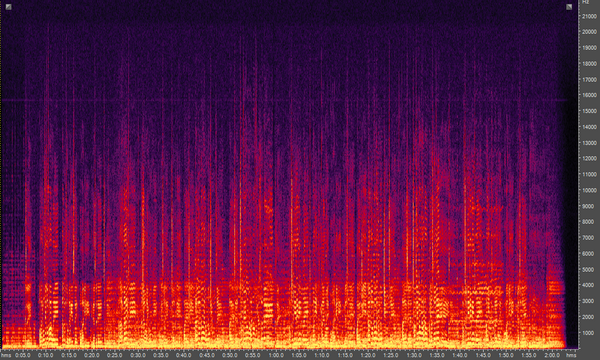
Das Spektrum wird nicht so dargestellt, wie wir es bisher kennen, sondern die Frequenzen (Tonhöhen) werden vertikal (nach oben) dargestellt. Die Lautstärke wird durch die Farbe beschrieben: gelb ist sehr laut und violett ist leise. In der Horizontalen wird das Spektrum des Liedes in der Zeit (h:mm:ss) dargestellt, d.h. wie das Lied abläuft.

Im Spektrum sind horizontale Linien zu sehen. Das sind die "Noten" des Liedes.

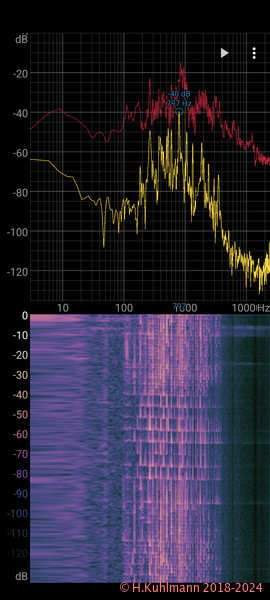
Die App Spectroid zeigt das Spektrum der aktuellen Geräuschkulisse auf dem Smartphone an.

Im oberen Teil wird das aktuelle Spektrum gelb dargestellt. Die lautesten Stellen sind rot.

Im unteren Teil wird das Spektrum als Wasserfall über der Zeit dargestellt. Der Wasserfall entspricht der Spektraldarstellung in Bild 15, ist aber um 90° nach rechts gedreht. Die Zahlen links neben dem Wasserfall sind keine Zeitangaben, sondern sollen die Farben beschreiben.

Im Wasserfall sind die "Noten" eines Klavierstücks gut zu erkennen. Auch gleichzeitig angeschlagene Töne sind erkennbar.

Im gelben Spektrum ist gut zu erkennen, dass reale Spektren nicht wie oben beschrieben aussehen, sondern verschmiert sind und Rauschen enthalten. Die Spitzen des Spektrums sind die Linien unserer Darstellung.

Die Wirkung können wir leicht untersuchen:

Einen Ton pfeifen.	Das ergibt eine Spitze im Spektrum und eine Linie im Wasserfall.
Einen Ton singen.	Das ergibt mehrere Spitzen im Spektrum und mehrere Linien im Wasserfall. Das sind die harmonischen Linien der Stimme.
Zischen.	Es gibt keine klaren Linien, sondern ein verschmiertes Spektrum, Rauschen.

Transformation moderner Musik und Sprache

Leider ist die Datenmenge im Spektralbereich nicht immer geringer als im Zeitbereich. Besonders problematisch sind Sprache und Geräusche.

• Grundsätzlich stellt sich die Frage: Wie können wir Sprache und Geräusche mit Noten beschreiben?

Transformation von Sprache in den Spektralbereich.

Einige von uns ahnen, dass dies etwas, das wir alle beherrschen.

Natürlich: Die Transformation von Sprache in den Spektralbereich ist das Schreiben und zurück in den Zeitbereich ist das Lesen.

Die Automatisierung von Lesen und Hören wird durch eine Zwischentransformation erreicht.

Die technologische Darstellung des Spektrums sind nicht etwa Buchstaben, sondern Phoneme. Die automatische Erkennung und Erzeugung von Sprache basiert auf Phonemen.

Wir kennen die Noten der Sprache: Buchstaben. Die Aussprache ist damit nur unzureichend beschrieben. Besser ist die Lautschrift: [ˈlaʊ̯tʃrɪft]. Dies sind im Prinzip die Phoneme.

Ein Text wird in eine Folge von Phonemen umgewandelt und diese werden "gesprochen".

Beim Hören werden die Phoneme erkannt und in Text umgewandelt.

In der Sprache, aber auch in der modernen Musik treten Klänge mit komplexen Spektren auf.

Das merkwürdige Spektrum in Bild 16 enthält nicht nur alle Töne der drei Oktaven, sondern auch alle möglichen dazwischen. Der graue Balken stellt das Spektrum dar. Es ist das Spektrum des Rauschens, des sch der Sprache. Das Spektrum von Rauschen besteht nicht mehr aus einzelnen Linien (Noten), sondern das Spektrum ist über alle Töne (Frequenzen) verteilt.

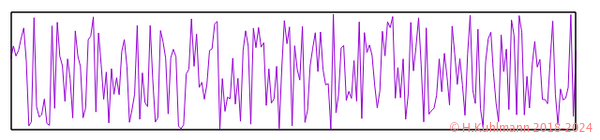
Rauschen

Die Zeitdarstellung des Rauschens ist schlimmer als Chaos.

In der Musik haben wir es oft mit einem Gemisch von Tönen (nach Noten) zu tun, aber auch mit Geräuschen. Ein Becken wird geschlagen oder eine Raschel betätigt. Wir betrachten hier beispielhaft Töne in einem Rauschen.

Werden gleichzeitig mit dem Rauschen auch Töne abgespielt, so überlagern sich die Spektren.

Ähnlich verhält es sich in der Zeitdarstellung.

Rauschen und Töne

Das Spektrum von Musik mit Rauschen umfasst nicht nur wenige Noten, sondern ist genauso umfangreich und komplex wie die Musik in der Zeitdarstellung.

• Der Vorteil, komplexe Klänge mit wenigen Daten darstellen zu können, gilt nicht für Rauschen:

Das Spektrum umfasst genauso viele Daten wie die Zeitdarstellung.

Das Rauschen in den Griff bekommen

Seit 1982 beschäftigen sich Forscher am Fraunhofer-Instituts in Erlangen mit diesem Problem.

Zunächst wird eine Fourier-Transformation durchgeführt. Das Ergebnis ist z.B. ein Spektrum wie in Bild 18.

Der Bereich um jede Note wird einfach dieser Note (Notenlinie) zugeordnet, in ihr zusammengefasst, komprimiert.

Bild 20 zeigt das komprimierte Spektrum aus Bild 18, wobei das Rauschen durch dicht beieinander liegende Töne (blau) ersetzt wurde. An den Stellen, an denen im Spektrum von Bild 18 ein Ton auftrat, wurde das Rauschen ignoriert.

Wir können es uns so vorstellen, dass auf einem Klavier alle Tasten gleichzeitig angeschlagen werden und auf einem zweiten Klavier drei Töne lauter. Das ist natürlich kein perfektes Rauschen, aber es kommt dem sehr nahe.

Das nächste Hörbeispiel besteht aus den zwölf Tönen einer Oktave. Es klingt schrecklich, aber das Rauschen ist erkennbar.

Rauschen mit den zwölf Tönen einer Oktave

Wenn wir mehr Oktaven nehmen, kommen wir dem Rauschen schon sehr nahe.

Rauschen mit den sechzig Tönen von fünf Oktaven

Menschen hören ungenau

Dass wir Menschen nicht beliebig genau hören können, machten sich die Erlanger Forscher zunutze.

• Welche Töne können wir noch unterscheiden?

• Wie laut muss ein Ton sein, damit wir ihn noch wahrnehmen?

• Welche Tonhöhen können wir hören?

Es zeigt sich, dass wir pro Oktave deutlich mehr Töne unterscheiden können als die zwölf Noten-Töne einer Oktave. Aber mehr als 50 Töne einer Oktave können wir nicht unterscheiden, oft sind es sogar weniger.

Bei MP3 werden zwischen die normalen Noten noch zusätzliche Töne für das Rauschen eingefügt. Der Tonumfang von MP3 umfasst etwa zehn Oktaven. Das sind 120 verschiedene Noten. MP3 unterscheidet 576 Töne. Tatsächlich werden die Töne, die den Noten zugeordnet sind, nicht getrennt betrachtet.

Unsere Fähigkeit oder Unfähigkeit des Wahrnehmens von Musik, Sprache und Geräusche wahrzunehmen, wird durch ein psychoakustisches Modell beschrieben. Die Unfähigkeiten werden insbesondere dazu benutzt, nicht Wahrnehmbares zu vernachlässigen.

Rauschen in der Musik

Wir betrachten Rauschen aus der Sicht von Musikern, von Musikern, die Rauschen mit der Hand machen mussten.

Im Folgenden Stück hören wir zu Beginn, wie alle zusammen durch Klatschen ein Rauschen erzeugen.

Richard Strauss hat in seiner Alpensinfonie, im ersten Abschnitt - Nacht - die Dunkelheit durch einen undurchsichtigen Klangschleier, der im Hintergrund rauscht, dargestellt. Die Streicher spielen fasst alle durcheinander.

Dieser Teil ist technisch interessant:

Strauss hat das Spektrum der rauschenden Streicher mit Lücken versehen, in die das Spektrum der Bläser passt.

Und nach drei Minuten geht die Sonne auf

Mathematische Tricks

Ein mathematischer Trick beruht auf der Beobachtung, dass bestimmte Zahlen in den aufgezeichneten Daten häufiger vorkommen (Jetzt folgen 12-mal 176448).

Ein anderer Trick ist eigentlich ein alter Hut. Seit 1865 gibt es den Morse-Code. (Siehe https://de.wikipedia.org/wiki/Morsezeichen#Standard-Codetabelle).

   da da   da da da   di da di   di

Der Code ordnet den Buchstaben eine Folge von kurzen und langen Zeichen zu. Die Anzahl der Zeichen pro Buchstabe variiert zwischen 1 und 4. Dem sehr häufig verwendeten Buchstaben E ist nur ein Zeichen di zugeordnet, T ist da. Das Y ist da-di-da-da. Das spart Zeit/Platz.

Auf diesem Verfahren basieren die bekannten Programme zum Komprimieren von Daten, die sogenannten Zipper. Während der Morse-Code den Zeichen einen festen Code zuordnet, wird beim Zippen ein Wörterbuch erstellt und den Wörtern ein Code zugewiesen. Wörterbuch und Code werden ständig an den aktuellen Text angepasst.

Mit ähnlichen Codes kann die Datenmenge einer Musikdatei weiter reduziert werden.

• Das angewandte Verfahren nennt sich Huffman-Kodierung.

Würden diese mathematischen Verfahren nur im Zeitbereich angewendet, könnte die Datenmenge auf etwa die Hälfte reduziert werden. MP3 schafft es mit der Fourier-Transformation auf ein Zehntel!

• Beim Zippen gehen keine Informationen verloren. Bei gezippten und wieder entzippten Musikdateien (WAV) ändert sich der Klang nicht.

• MP3 verändert den Klang - allerdings nur geringfügig.

Bei MP3 werden mathematische Tricks auf die Daten im Spektralbereich angewendet. Bei MP3 wird im Prinzip die Lautstärke der 576 möglichen Töne/Noten gezippt.

All dies setzt leistungsfähige Computer voraus - bei der Transformation in den Spektralbereich. Na ja, ein Smartphone schafft das heute mit links. Die Transformation vom Spektral- in den Zeitbereich ist dagegen relativ einfach. MP3-Player sind klein und handlich.

Unzulänglichkeiten von MP3

Das Zusammenfassen ähnlicher Töne wurde bei den ersten MP3-Verfahren relativ rigoros gehandhabt. Den meisten Menschen fällt das nicht auf. Einige Musiker mit geschultem Gehör können diese Unterschiede wahrnehmen. Am problematischsten ist die Wiedergabe von Sprache und Geräuschen. Inzwischen gibt es Verfahren, die wesentlich bessere Ergebnisse liefern. Sie unterscheiden sich hauptsächlich darin, wie und welche Daten aus dem Spektrum der 576 Töne/Noten ignoriert werden.

Musik langsam abspielen

Für einen Musiker ist es kein Problem, ein Musikstück langsamer zu spielen. Jeder Ton erklingt länger. Für den Zuhörer klingt das Musikstück gleich, nur langsamer.

Wenn aber ein Musikstück, das im Zeitbereich aufgenommen wurde, langsamer abgespielt wird, ändert sich nicht nur die Dauer der einzelnen Töne, sondern auch der Klang. Alle Töne klingen tiefer. Die Musik erklingt in Zeitlupe.

MP3 ist wie das Spielen nach Noten eine Transformation vom Spektralbereich in den Zeitbereich. Der Klang eines Musikstücks ändert sich nicht wesentlich, wenn es langsamer abgespielt wird.

Time-Stretching

Moderne Player können auch WAV-Dateien und CDs langsam abspielen, ohne dass sich der Klang oder die Tonhöhe wesentlich verändert.

Das Verfahren beruht auf Fourier-Transformation und wird als Time-Stretching bezeichnet.

Zunächst findet eine Transformation aus dem Zeitbereich in den Spektralbereich statt. Bei der anschließenden Transformation vom Spektral- in den Zeitbereich werden alle Töne/Noten einfach länger gespielt.

Im Folgenden wird ein Ausschnitt zuerst mit normaler Geschwindigkeit und dann mit halber Geschwindigkeit abgespielt.

Wow im Original

Wow mit 1/2 im Zeitbereich

Wow mit 1/2 im Spektralbereich (Time-Stretching)

Zusammenfassung

• Zuerst beschäftigten wir uns mit vielen uns bekannten Methoden der Musikaufnahme und lernten die zugrundeliegenden Prinzipien kennen.

• Begriffe wie Spektral- und Zeitdarstellung wurden anhand von Beispielen erklärt.

• Noten als Spektraldarstellung

• Das Spielen von Musik als Zeitdarstellung

• Ausgehend von der gängigen Spektraldarstellung von Musik, den Noten, wurde die technische, mathematische Darstellung betrachtet.

• Die Spektraldarstellung von Musik ist in der Regel viel kompakter als die Zeitdarstellung.

• Sprache und Geräusche stellen ein Problem dar.

• Bei MP3 werden ähnliche Bereiche des Spektrums zu einem Wert (Note) zusammengefasst.

• Die historische Entwicklung der Musikaufzeichnung und die Intuition vieler Menschen wurden im MP3-Verfahren zusammengefasst.

• Das MP3-Verfahren automatisiert die Kopfarbeit von Musikern und Mathematikern
  - modern: digitalisiert.