Widerstand, Strom und Spannung (Ohm)

Zum Kopf

Ein Elektroniker kommt nicht weiter, ohne den Zusammenhang zwischen Widerstand, Strom und Spannung zu kennen. Er muss einige Formeln kennen und anwenden können. Ebenso wichtig ist es, dass er intuitiv beurteilen kann, wie diese drei Größen zusammenhängen. Dieses intuitive Vorgehen muss auf Erfahrung beruhen. Dazu gehört das Anwenden von Formeln.

Das Schaltbild

Bild 1: Strom- und Spannungspfeile an einem Widerstand

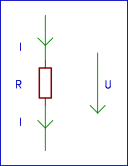
Wir haben einen Widerstand R, an dem eine Spannung U abfällt und durch den ein Strom I fließt.

Regeln

Wenn der Widerstand größer wird, wird der Strom bei gleicher Spannung kleiner.

Umgekehrt, wird der Strom größer, wenn der Widerstand kleiner wird.

Wird der Widerstand größer, so wird bei gleichem Strom die Spannung am Widerstand größer.

Umgekehrt, wird die Spannung kleiner, wenn der Widerstand kleiner wird.

Wird der Strom durch den Widerstand größer, wird die Spannung am Widerstand größer.

Umgekehrt, wird der Strom durch den Widerstand kleiner, wird die Spannung am Widerstand kleiner.

Steigt die Spannung am Widerstand, steigt auch der Strom durch den Widerstand.

Umgekehrt, fällt der Strom, wenn die Spannung kleiner wird.

Soll bei einer Spannung ein größerer Strom fließen, wird ein kleinerer Widerstand benötigt.

Umgekehrt, soll kleinerer Strom fließen, wird ein größerer Widerstand benötigt.

Faustregel

Ursache

Wirkung

Spannung steigt

Strom steigt

Widerstand steigt

Strom fällt

Widerstand steigt

Spannung steigt

Wir können Ursache und Wirkung umkehren. Wir können auch steigt gegen fällt tauschen.

Formeln

Das Tool Ohm unterstützt Berechnungen zum Ohmschen Gesetz.

Ohmsches Gesetz

Die obigen Regeln geben nur einen qualitativen Zusammenhang (größer, kleiner usw.) wieder. Wir können auch Widerstand, Strom und Spannung berechnen. Wenn zwei der drei Größen bekannt sind, können wir die dritte berechnen.

Strom berechnen

I = U / R

Spannung berechnen

U = R * I

Widerstand berechnen

R = U / I

Diesen Zusammenhang hat Georg Simon Ohm vor zweihundert Jahren entdeckt. Ihm zu Ehren nennen wir ihn das Ohmsche Gesetz.

Leistung am Widerstand

Die Leistung P am Widerstand ist

Leistung berechnen

   P = U * I
   P = U * U / R
   P = I * I * R

Maßeinheiten

Die obigen Formeln gelten für

Strom	in Ampere, A
Spannung	in Volt, V
Widerstand	in Ohm, Ω
Leistung	in Watt, W

Wir kennen auch Abkürzungen für die Einheiten:

Widerstand

1kΩ =    1000Ω
1MΩ = 1000000Ω = 1000kΩ

Spannung

1kV = 1000V
1mV = 0,001V
1V  = 1000mV

Strom

1kA  = 1000A
1mA  = 0,001A    = 1000µA
1µA  = 0,000001A = 0,001mA
1A   = 1000mA    = 1000000µA

Leistung

1kW  = 1000W
1mW  = 0,001W    = 1000µW
1µW  = 0,000001W = 0,001mW
1W   = 1000mW    = 1000000µW

Die Formeln sind einfach, wenn die folgenden vier Maßeinheiten zusammen verwendet werden.

I	R	U	P
A	Ω	V	W
mA	kΩ	V	W
µA	MΩ	V	W
mA	Ω	V	mW
µA	Ω	V	µW
A	Ω	mV	mW

Beispiele

Berechnung des Messwiderstands einer elektronischen Sicherung

Gültigkeit der Formeln

Der alte Ohm hat bereits darauf hingewiesen, dass seine Formeln nicht für alle Widerstände gelten.

Wir machen es umgekehrt und nennen die Widerstände, die den obigen Formeln entsprechen, ohmsche Widerstände.

Es gibt Widerstände, die den Ohmschen Formeln in keiner Weise entsprechen. Diese Widerstände werden als spannungsabhängige Widerstände (VDR) oder Varistoren bezeichnet. Für Varistoren gelten die Formeln nicht, wohl aber die Regeln.

Andere Widerstände sind von anderen Größen abhängig, z.B. von Licht und Temperatur.